前言
这篇文章主要是教会你如何快速了解高斯过程进行回归预测的,并没有太多的公式推导,只有简单的相关的概念的介绍,如果您要自己掌握并使用高斯过程进行一个简单的预测,当然还需要进行一些基础知识的学习,我会在文章最后推荐一些博主有关高斯过程详细介绍的文章。
话不多说,首先我们看一下面这道题目。这里该不会有人不知道“回归”的意思吧,简单讲回归就是一种拟合,把孤立的东西联系起来,找到规律,这就叫回归。正如题目所示,我们知道了六个点的纵坐标,要预测第七个点的纵坐标。我想很多人都知道线性回归的吧,也就是用y=kx+b来代表整个数据点的趋势,虽然数据点不能完全在这直线上,但是也可以通过这个表达式预测出第七个点(x=0.2)的纵坐标。但是记住,本篇文章是高斯过程回归预测呀!!!也就是我们要用高斯过程来进行回归并预测。接下来介绍一些基础的概率论的知识~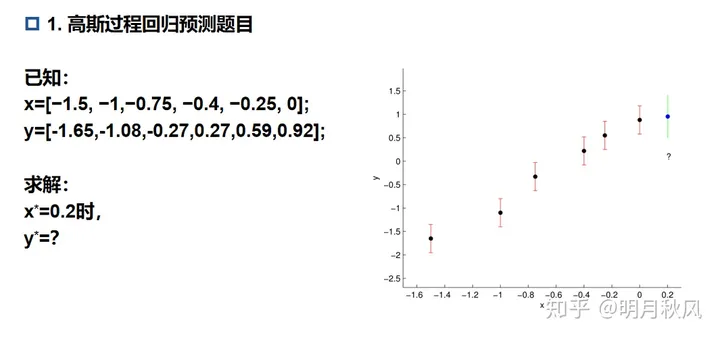
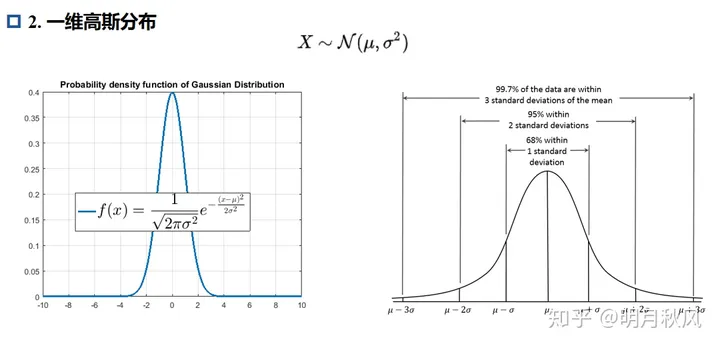
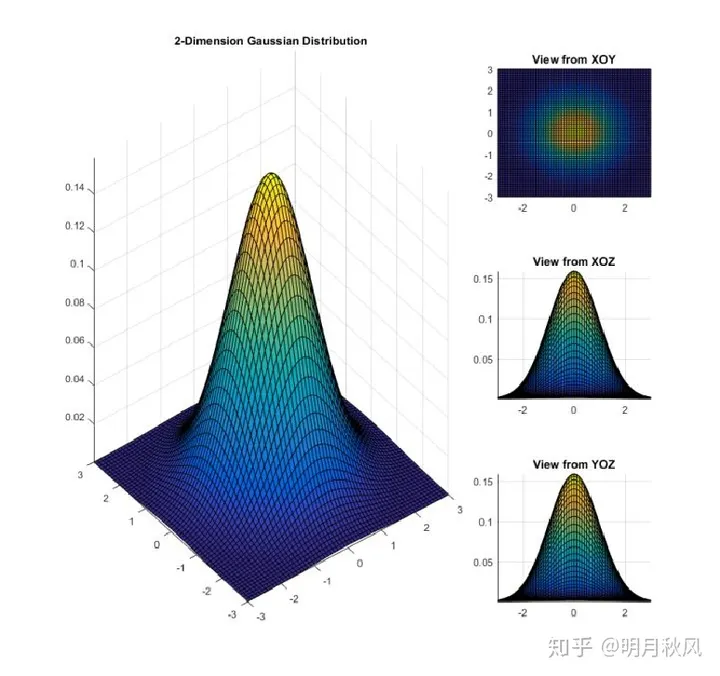
THE END













暂无评论内容