19. Evangelidis, G.D., Kounades-Bastian, D., Horaud, R., Psarakis, E.Z.: A generative
model for the joint registration of multiple point sets. In: ECCV 2014. (2014) 109–
122 2, 3, 9, 11
20. Horaud, R., Forbes, F., Yguel, M., Dewaele, G., Zhang, J.: Rigid and articulated
point registration with expectation conditional maximization. IEEE Trans. on
Pattern Analysis and Machine Intelligence 33(3) (2011) 587–602 2, 3, 9接上篇,这次介绍一下第二篇论文,Fast and Accurate Point Cloud Registration using Trees of Gaussian Mixtures
摘要:
先提了点云匹配的重要性,然后说他们在上篇文章的基础上,使用了HGMM搞出了一个很牛逼的新算法,取得了SOAT的速度和精度,同时可以自适应地在两个点云的关连子集里找到最适合的尺度。然后相比ICP和其他GMM方法,这种以树为基础的算法可以在对数时间完成点云的对应,同时动态地适应细节的层次,来最佳地匹配局部场景几何形状的复杂性和空间分布特征。我觉得这点很有意思,主要看看他们是怎么定义这个细节的层次,怎么样就可以不去遍历下面的子节点。还有一个特点,在第一篇文章说过了,这里GMM的协方差矩阵可以是各向异性的,通过使用基于PCA的新优化准则,可以很好地接近真MLE的解。
特点:
1.高效的数据关连;
2. 多尺度的适应性;
3. 鲁棒的逼近最大似然估计;
效果:
比当前算法(2018年时候的效果)在3d数据集上达到了一个数量级上的速度和精度提升。
这边放一个他们和其他算法对比:
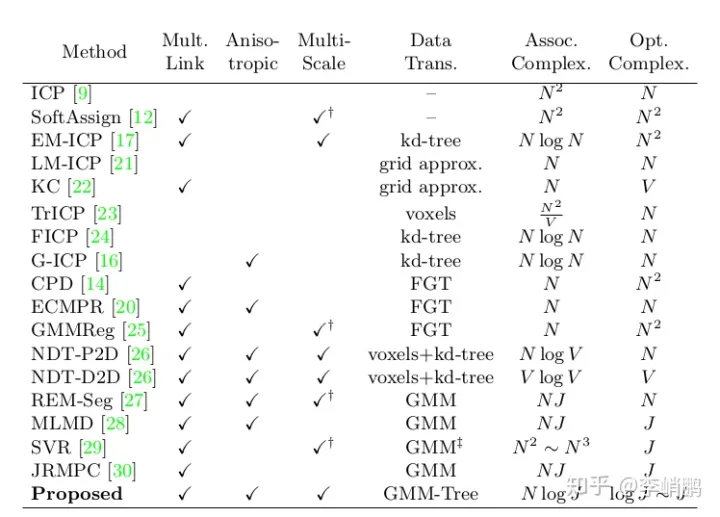
相比之下,可以看出E-step和M-step都达到了最佳的时间复杂度。
跳过了前两节,到第三节 Registration as Expectation Maximization
EM算法,是绝大多数基于统计的匹配方法的理论基础,并在特定的假设下概括了ICP,所以都可以把ICP和统计方法一起对比。在不能直接通过变量最大化数据的概率,而通可以通过一组潜变量为条件时最大化期望联合概率的情况时,EM算法可以用来做最大似然估计的优化。
在点云匹配情况下,我们的所求变量为两个点云间的转换矩阵T,潜变量是点和点云模型的联系。数学上的表示为在给定的两个点云 ,Z1,Z2Z_{1},Z_{2} ,在一组转换矩阵T中最大化 Z2Z_{2} 在从 Z1Z_{1}推导出的概率模型 ΘZ1\Theta_{Z_{1}} 的概率。用公式表达起来就很方便了。
T~=argmaxTP(T(Z2)|Θ¯Z1)\tilde{T} = argmax_{T} P(T(Z_{2})| \bar{\Theta}_{Z_{1}}) 1
对转换矩阵 T~\tilde{T} 的最大似然估计,是最大化转换过来的点云 T(Z2)T(Z_{2}) 在 从Z1Z_{1}的空间分布推导出的模型 ΘZ1\Theta_{Z_{1}} 空间似然的概率表示的估计。(翻译成人话,就是使得转换过的 Z2Z_{2} 尽可能地和 Z1Z_{1}重合,这边说这么复杂,是为了从概率的角度来解释,但我换成ICP的表述,就简单易懂一些。)
当我们用GMM来表示 ΘZ1\Theta_{Z_{1}} 时,即用J个带权重的高斯分布的凸组合来表示,那么一个点在 ΘZ1\Theta_{Z_{1}} 的概率分布可以表示成点在这些高斯分布的加权和:
p(z|ΘZ1)=∑j=1JπjN(z|Θj)p( z |\Theta_{Z_{1}}) = \sum_{j =1 }^{J}{ \pi_{j} N(z |\Theta_{j})} 2
同样需要引入一组潜在的对应变量C=[cij]C = [c_{ij} ] 表明 Z2Z_{2} 中的点 ziz_{i} 与世界模型 ΘZ1\Theta_{Z_{1}}中的J个子分布的对应关系,其实就相当于ICP在找对应点的过程,,而最大化期望的条件分布相当于ICP中的最小化距离。
E[cij=1]=πjN(zi|θj)∑k=1JπkN(zi|θk)E[c_{ij} =1 ] = \frac{\pi_{j} N(z_{i}|\theta_{j})}{\sum_{k=1}^{J}{\pi_{k} N(z_{i}|\theta_{k})}} 3
4. Hierarchical Gaussian MIxture Mahalanobis Estimation
这节是大头,讲怎么用HGMM这个树模型去帮助EM算法的。
4,1 E step: 自适应的树搜索
先回忆一下树的搜索:深度优先搜索(DFS)、广度优先搜索(WFS)。这边是用递归的DFS,从而可以在对数时间完成数据的似然联系,即求得公式3,而且这个搜索可以提前终止,在已经找到了最适合的尺度能把数据点和层次化的模型联系起来。
GMM树每个父节点都有八个子节点,感觉和八叉树的形式有些像。而这个八叉GMM树的每个节点都有两个含义:1. 点云的一个概率划分;2. 点云中一个分区的统计描述。E-step使用到了这两个性质,利用1 实现了高效的搜索算法,利用2实现了启发式的尺度选择。
a)高效的对数搜索
GMM里的每一层形成了一个在更精细层级的粒度与细节上的统计学划分。关键的是一个点z对一个特定节点的期望等于对这个父节点的所有子节点的期望和。利用这点可以帮助我们简化计算,只要我们发现点在一个节点的概率低于阈值,那么就可以终止对这个节点的子节点的期望计算了。当我们只计算最大似然路径时,我们的时间复杂度就从O(N*J)简化到O(logJ)。
b)多尺度的自适应性
为了匹配真实场景不同部分的尺度复杂性,论文中利用到了GMM树可以多层次表示的优点来防止过拟合。我觉得这篇论文的亮点在于这点:提出了一种去检查当前模型的几何复杂性的定义。
Complexity(Θ)=λmin∑i=13λiComplexity(\Theta) = \frac{\lambda_{min}}{\sum_{i=1}^{3}{\lambda_{i}}} 4
其中λ\lambda 为对应协方差矩阵的特征值,
当Complexity(·) 小于通过实验确定的阈值λC\lambda_{C} =0.01时,就终止搜索。
物理含义:高斯模型的协方差矩阵的特征值可以表明高斯模型的分布特征。为什么这么说呢?
高斯模型的标准形式为:均值为0向量,协方差为单位矩阵I。
标准高斯模型通过线性缩放,旋转可以得到任意高斯模型。具体推导参见:
在这里,我引用大佬的文章里的结论:多元正态分布的概率密度是由协方差矩阵的特征向量控制旋转(rotation),特征值控制尺度(scale),,均值向量会控制概率密度的位置。
当一个特征值已经很小的时候,这个高斯分布可以认为是一个平面。而平面(线)就是我们想要的最简结构了。那么我们就不需要继续往下去计算子模型了。

算法1是文章里提供的伪代码,写的很清晰啦,
4.2 M step:Mahalanobis Estimation
论文提出了一种新的寻找最优变换矩阵的M Step.
M step干的就是最大化联合概率分布。
首先,给定 N个点 ziz_{i} 和 J个分类 Θj∈Θ~Z1\Theta_{j}\in \tilde{\Theta}_{Z_{1}} 再引入一个 N*J的点类对应集合 C={cij}C = \left\{ c_{ij} \right\} ,则完全联合概率可写为:
lnP(T(Z),C|Θ)=∑i=1N∑j=1Jcij{lnπj+lnN(T(zi)|Θj)}ln P\left( T\left( Z \right),C |\Theta \right) = \sum_{i=1}^{N}{\sum_{j=1}^{J}{c_{ij}\left\{ln\pi_{j} +lnN\left( T\left(z_{i} \right)|\Theta_{j} \right)\right\}}} 5
在E-step中,我们在当前后验中,定义 γijdef⇒E[cij]\gamma_{ij}def\Rightarrow E\left[ c_{ij} \right] 。在固定所有 γij\gamma_{ij} 的情况下,求5这个联合条件概率关于T的最大似然函数,
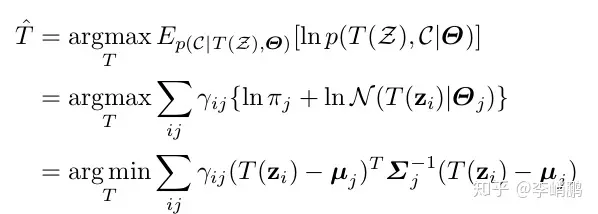
于是,在两个点云间的最大似然变换矩阵T为一个最小化 点云Z2Z_{2}的点和 ΘZ1\Theta_{Z_{1}}的独立类簇之间平方马氏距离的加权和。这里的权重是通过计算在给定当前对T的最佳猜测的期望对应而确定。
马氏距离:Mahalanobis Distance
这个概念我之前不知道,先放下定义:
马氏距离是由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出的,表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的)并且是尺度无关的(scale-invariant),即独立于测量尺度。
对于一个均值为
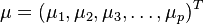
,协方差矩阵为Σ的多变量矢量
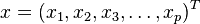
,其马氏距离为
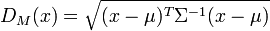
对比上面的公式6,可以发现正好是 DM(x)D_{M}\left( x \right) 的平方形式。
根据在参考文献中的数学证明,如果我们把T唯一地限制到所有刚性变换的集合里,即
T={R∈SO(3),t3∗1}T = \left\{ R\in SO\left( 3 \right),t_{3*1} \right\}
可以进一步地把点和簇上的双重和减少为簇上的单个和。
T~=argminT∑ijγij(T(zi)−μj)T∑j−1(T(zi)−μj)\tilde{T} =argmin_{T}\sum_{ij}^{}{\gamma_{ij}}(T(z_{i})-\mu_{j})^{T}\sum_{j}^{-1}(T(z_{i})-\mu_{j})
T~=argminT∑jπj∗(T(μj∗)−μj)T∑j−1(T(μj∗)−μj)\tilde{T} =argmin_{T}\sum_{j}^{}{\pi_{j}^{*}} (T(\mu_{j}^{*})-\mu_{j})^{T}\sum_{j}^{-1}(T(\mu_{j}^{*})-\mu_{j})
其中, πj∗=∑iγijN\pi_{j}^{*} = \frac{\sum_{i}^{}{\gamma_{ij}}}{N} , μj∗=∑iγijzi∑iγij\mu_{j}^{*} = \frac{\sum_{i}^{}{\gamma_{ij}z_{i}}}{\sum_{i}^{}{\gamma_{ij}}} 这里是把点 ziz_{i} 按对应关系做了加权平均。
现在的式子里就只有 高斯模型的J了,用E-step得到的Mj0M_{j}^{0} , Mj1M_{j}^{1} 来代替
T~=argminT∑jMj0(T(Mj1Mj0)−μj)T∑j−1(T(Mj1Mj0)−μj)\tilde{T} =argmin_{T}\sum_{j}^{}{M_{j}^{0}} (T(\frac{M_{j}^{1}}{M_{j}^{0}})-\mu_{j})^{T}\sum_{j}^{-1}(T(\frac{M_{j}^{1}}{M_{j}^{0}})-\mu_{j}) 8
这个等式还是一个比较复杂的形式,对每个协方差矩阵做分解,使用PCA得到它的特征值 λ\lambda 和特征向量 nn。之后作者重写了等式8的最大似然估计准则里的内部马氏距离。
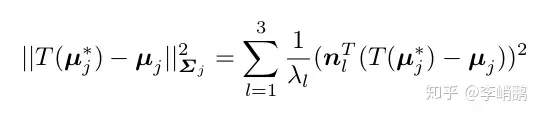
那么可以把形式转换为
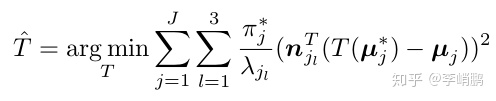
这边就完成了一个转换,本来要计算在最大似然准则里的每个类的马氏距离,现在就不用这么麻烦的计算了。这时候只要计算三个独立的点-面距离的加权和,而且权重是特征值的倒数,特征向量是对应平面的的法向量。这时候,ICP中计算点-面距离的方法可以拿来用,而且我们能很轻易地得到平面,只要做一个3*3矩阵的分解就好了.
现在只需要求解等式12即可。文章中使用Low, K.L.: Linear least-squares optimization for point-to-plane icp surface regis-tration. Chapel Hill, University of North Carolina 4 (2004) 10 提出的线性最小二乘法,因为基于GMM的匹配方法是局部的,会在大姿态位移中发散的事实,使用了小角度假设,对旋转矩阵R进行了线性化。我觉得这块或许可以优化下。
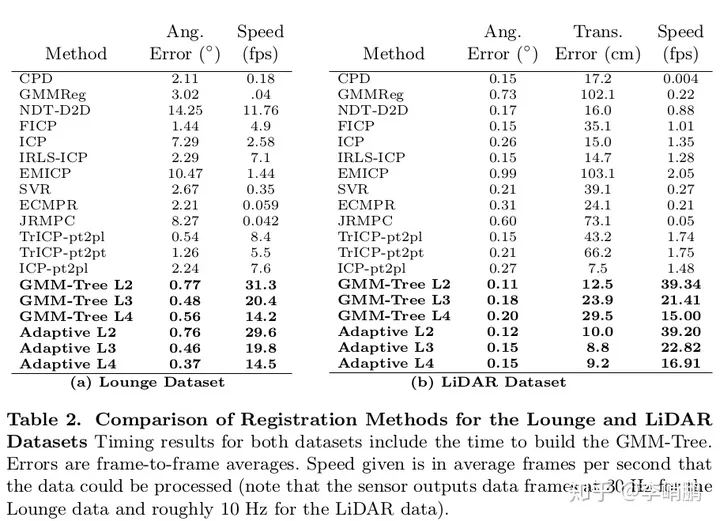
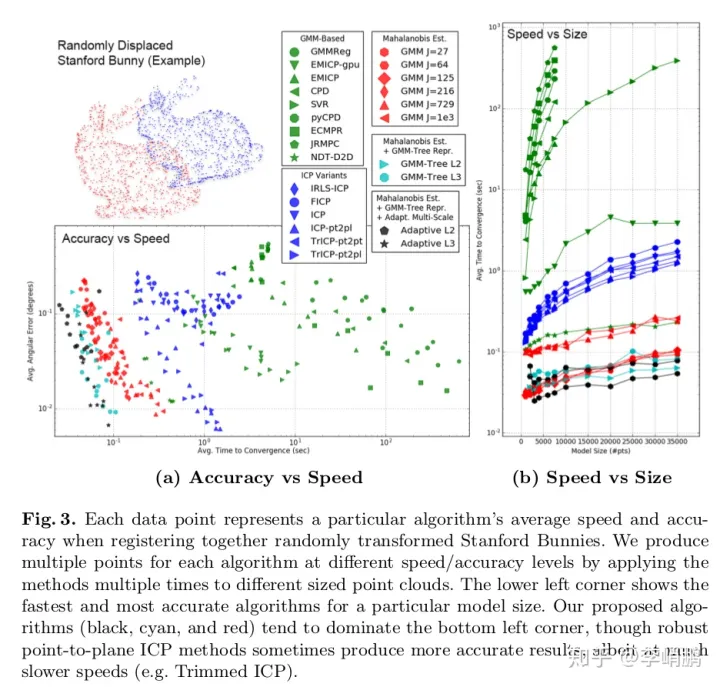
5.速度和精度
直接上表格了,感觉表现挺好的,在GPU的加速下可以达到实时性的要求。
结语:
这两篇文章做了比较出色的工作,感觉在工程中实现的话会提高定位的精度。不过也没关注最新的paper,希望更看到更多有意思的文章,然后我可以抱抱大腿。哈哈哈。














暂无评论内容