一分钟详解PCL中点云配准技术

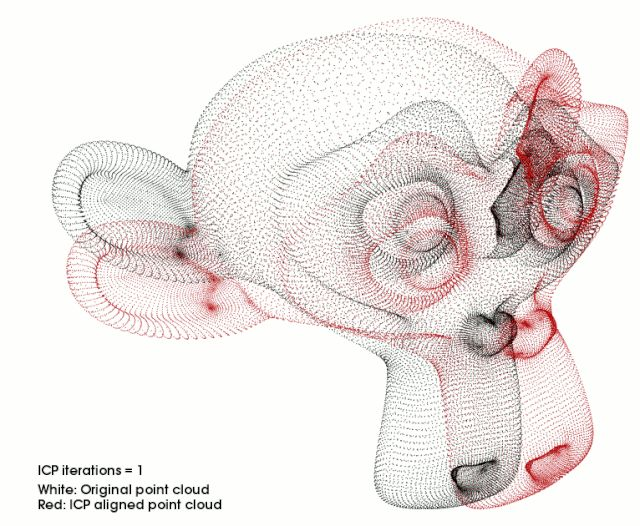
原文首发于微信公众号「３D视觉工坊」：一分钟详解PCL中点云配准技术

本文是对前两篇文章：点云配准（一 两两配准）以及3D点云（二 多福点云配准）的补充，希望可以在一定程度上帮助大家对点云配准理解地更为深刻。

一 PCL中点云配准技术的简单实现

在同一文件夹下，有测试数据文件monkey.ply，该文件是利用Blender创建的默认Monkey模型。

利用如下代码，将初始点云（图中绿色点云）进行旋转平移，得到目标点云（图中红色点云）。

// 旋转矩阵的具体定义 (请参考 https://en.wikipedia.org/wiki/Rotation_matrix

)

double theta = M_PI / 20; // 设置旋转弧度的角度

transformation_matrix (0, 0) = cos (theta);

transformation_matrix (0, 1) = -sin (theta);

transformation_matrix (1, 0) = sin (theta);

transformation_matrix (1, 1) = cos (theta);

// 设置平移矩阵

transformation_matrix (0, 3) = 0.0;

transformation_matrix (1, 3) = 0.0;

transformation_matrix (2, 3) = 4.0;

// 执行初始变换

pcl::transformPointCloud (*cloud_in, *cloud_icp, transformation_matrix);

pcl::PointCloud::Ptr cloud_xyz(new pcl::PointCloud());

pcl::io::savePCDFileASCII(“./monkey_rotated_trans.pcd”,*cloud_icp);

完整的PCL点云配准分为粗配准与精配准两个阶段，（此处参考博文：https://blog.csdn.net/peach_blossom/article/details/78506184，在此，特别感谢作者的无私分享，才能让我们这些后来人少走弯路），示例demo如下（稍作修改）。

#include

#include

#include

#include

#include

#include

#include

#include

#include

#include

#include

#include

#include

typedef pcl::PointXYZ PointT;

typedef pcl::PointCloud PointCloud;

//点云可视化

void visualize_pcd(PointCloud::Ptr pcd_src,

PointCloud::Ptr pcd_tgt,

PointCloud::Ptr pcd_final)

{

// Create a PCLVisualizer object

pcl::visualization::PCLVisualizer viewer(“registration Viewer”);

//viewer.createViewPort (0.0, 0, 0.5, 1.0, vp_1);

// viewer.createViewPort (0.5, 0, 1.0, 1.0, vp_2);

pcl::visualization::PointCloudColorHandlerCustom src_h (pcd_src, 0, 255, 0);

pcl::visualization::PointCloudColorHandlerCustom tgt_h (pcd_tgt, 255, 0, 0);

pcl::visualization::PointCloudColorHandlerCustom final_h (pcd_final, 0, 0, 255);

viewer.addPointCloud (pcd_src, src_h, “source cloud”);

viewer.addPointCloud (pcd_tgt, tgt_h, “tgt cloud”);

viewer.addPointCloud (pcd_final, final_h, “final cloud”);

//viewer.addCoordinateSystem(1.0);

while (!viewer.wasStopped())

{

viewer.spinOnce(100);

boost::this_thread::sleep(boost::posix_time::microseconds(10000));

}

}

//由旋转平移矩阵计算旋转角度

void Matrix2Angle (Eigen::Matrix4f &result_trans,Eigen::Vector3f &result_angle)

{

double ax,ay,az;

if (result_trans(2,0)==1 || result_trans(2,0)==-1)

{

az=0;

double dlta;

dlta=atan2(result_trans(0,1),result_trans(0,2));

if (result_trans(2,0)==-1)

{

ay=M_PI/2;

ax=az+dlta;

}

else

{

ay=-M_PI/2;

ax=-az+dlta;

}

}

else

{

ay=-asin(result_trans(2,0));

ax=atan2(result_trans(2,1)/cos(ay),result_trans(2,2)/cos(ay));

az=atan2(result_trans(1,0)/cos(ay),result_trans(0,0)/cos(ay));

}

result_angle<

}

void doRegistration(std::string src_cloud_path,std::string tgt_cloud_path, Eigen::Matrix4f &icp_trans)

{

//加载点云文件

PointCloud::Ptr cloud_src_origin (new PointCloud);//原点云，待配准

pcl::io::loadPLYFile (src_cloud_path,*cloud_src_origin);

PointCloud::Ptr cloud_tgt_origin (new PointCloud);//目标点云

pcl::io::loadPCDFile (tgt_cloud_path,*cloud_tgt_origin);

clock_t start=clock();

//去除NAN点

std::vector indices_src; //保存去除的点的索引

pcl::removeNaNFromPointCloud(*cloud_src_origin,*cloud_src_origin, indices_src);

std::cout<<“remove *cloud_src_origin nan”<

//下采样滤波

pcl::VoxelGrid voxel_grid;

voxel_grid.setLeafSize(0.014,0.014,0.014);

voxel_grid.setInputCloud(cloud_src_origin);

PointCloud::Ptr cloud_src (new PointCloud);

voxel_grid.filter(*cloud_src);

std::cout<<“down size *cloud_src_origin from “<size()<<“to”<size()<

//pcl::io::savePCDFileASCII(“monkey_src_down.pcd”,*cloud_src);

//计算表面法线

pcl::NormalEstimation ne_src;

ne_src.setInputCloud(cloud_src);

pcl::search::KdTree< pcl::PointXYZ>::Ptr tree_src(new pcl::search::KdTree< pcl::PointXYZ>());

ne_src.setSearchMethod(tree_src);

pcl::PointCloud::Ptr cloud_src_normals(new pcl::PointCloud< pcl::Normal>);

ne_src.setRadiusSearch(0.02);

ne_src.compute(*cloud_src_normals);

std::vector indices_tgt;

pcl::removeNaNFromPointCloud(*cloud_tgt_origin,*cloud_tgt_origin, indices_tgt);

std::cout<<“remove *cloud_tgt_origin nan”<

pcl::VoxelGrid voxel_grid_2;

voxel_grid_2.setLeafSize(0.01,0.01,0.01);

voxel_grid_2.setInputCloud(cloud_tgt_origin);

PointCloud::Ptr cloud_tgt (new PointCloud);

voxel_grid_2.filter(*cloud_tgt);

std::cout<<“down size *cloud_tgt_origin.pcd from “<size()<<“to”<size()<

//pcl::io::savePCDFileASCII(“monkey_tgt_down.pcd”,*cloud_tgt);

pcl::NormalEstimation ne_tgt;

ne_tgt.setInputCloud(cloud_tgt);

pcl::search::KdTree< pcl::PointXYZ>::Ptr tree_tgt(new pcl::search::KdTree< pcl::PointXYZ>());

ne_tgt.setSearchMethod(tree_tgt);

pcl::PointCloud::Ptr cloud_tgt_normals(new pcl::PointCloud< pcl::Normal>);

//ne_tgt.setKSearch(20);

ne_tgt.setRadiusSearch(0.02);

ne_tgt.compute(*cloud_tgt_normals);

//计算FPFH

pcl::FPFHEstimation fpfh_src;

fpfh_src.setInputCloud(cloud_src);

fpfh_src.setInputNormals(cloud_src_normals);

pcl::search::KdTree::Ptr tree_src_fpfh (new pcl::search::KdTree);

fpfh_src.setSearchMethod(tree_src_fpfh);

pcl::PointCloud::Ptr fpfhs_src(new pcl::PointCloud());

fpfh_src.setRadiusSearch(0.05);

fpfh_src.compute(*fpfhs_src);

std::cout<<“compute *cloud_src fpfh”<

pcl::FPFHEstimation fpfh_tgt;

fpfh_tgt.setInputCloud(cloud_tgt);

fpfh_tgt.setInputNormals(cloud_tgt_normals);

pcl::search::KdTree::Ptr tree_tgt_fpfh (new pcl::search::KdTree);

fpfh_tgt.setSearchMethod(tree_tgt_fpfh);

pcl::PointCloud::Ptr fpfhs_tgt(new pcl::PointCloud());

fpfh_tgt.setRadiusSearch(0.05);

fpfh_tgt.compute(*fpfhs_tgt);

std::cout<<“compute *cloud_tgt fpfh”<

//SAC配准

pcl::SampleConsensusInitialAlignment scia;

scia.setInputSource(cloud_src);

scia.setInputTarget(cloud_tgt);

scia.setSourceFeatures(fpfhs_src);

scia.setTargetFeatures(fpfhs_tgt);

//scia.setMinSampleDistance(1);

//scia.setNumberOfSamples(2);

//scia.setCorrespondenceRandomness(20);

PointCloud::Ptr sac_result (new PointCloud);

scia.align(*sac_result);

std::cout <<“sac has converged:”<

Eigen::Matrix4f sac_trans;

sac_trans=scia.getFinalTransformation();

std::cout<

//pcl::io::savePCDFileASCII(“monkey_transformed_sac.pcd”,*sac_result);

clock_t sac_time=clock();

//icp配准

PointCloud::Ptr icp_result (new PointCloud);

pcl::IterativeClosestPoint icp;

icp.setInputSource(cloud_src);

icp.setInputTarget(cloud_tgt_origin);

icp.setMaxCorrespondenceDistance (0.04);

// 最大迭代次数

icp.setMaximumIterations (2);

// 两次变化矩阵之间的差值

icp.setTransformationEpsilon (1e-10);

// 均方误差

icp.setEuclideanFitnessEpsilon (0.2);

icp.align(*icp_result,sac_trans);

clock_t end=clock();

cout<<“total time: “<<(double)(end-start)/(double)CLOCKS_PER_SEC<<” s”<

cout<<“sac time: “<<(double)(sac_time-start)/(double)CLOCKS_PER_SEC<<” s”<

cout<<“icp time: “<<(double)(end-sac_time)/(double)CLOCKS_PER_SEC<<” s”<

std::cout << “ICP has converged:” << icp.hasConverged()

<< ” score: ” << icp.getFitnessScore() << std::endl;

icp_trans=icp.getFinalTransformation();

//cout<<“ransformationProbability”<

std::cout<

//使用创建的变换对未过滤的输入点云进行变换

pcl::transformPointCloud(*cloud_src_origin, *icp_result, icp_trans);

//保存转换的输入点云

//pcl::io::savePCDFileASCII(“monkey_transformed_sac_ndt.pcd”, *icp_result);

//计算误差

Eigen::Vector3f ANGLE_origin;

ANGLE_origin<<0,0,M_PI/5;

double error_x,error_y,error_z;

Eigen::Vector3f ANGLE_result;

Matrix2Angle(icp_trans,ANGLE_result);

error_x=fabs(ANGLE_result(0))-fabs(ANGLE_origin(0));

error_y=fabs(ANGLE_result(1))-fabs(ANGLE_origin(1));

error_z=fabs(ANGLE_result(2))-fabs(ANGLE_origin(2));

cout<<“original angle in x y z:\n”<

cout<<“error in aixs_x: “<

//可视化

visualize_pcd(cloud_src_origin,cloud_tgt_origin,icp_result);

}

int

main (int argc, char** argv)

{

std::string src_cloud_path=”../monkey.ply”;

std::string tgt_cloud_path=”../monkey_rotated_trans.pcd”;

Eigen::Matrix4f icp_trans;

doRegistration(src_cloud_path,tgt_cloud_path,icp_trans);

return (0);

}

运行后的效果图如下。

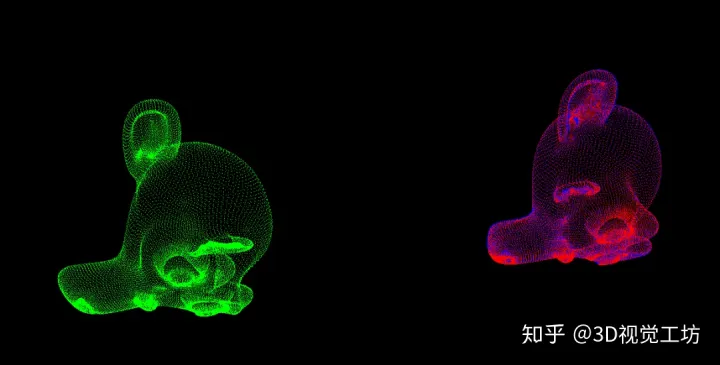
可以发现，程序中即使设置了最大迭代次数为2，但配准后的效果已经很好啦（红色点云与蓝色点云几乎已经重合）。

二 深剖PCL中配准技术细节

对于以上配准过程，大致可以总结如下：

第一步：加载点云；

第二步：下采样滤波；

第三步：计算表面法线；

第四步：计算FPFH；

第五步：SAC_IA粗配准；

第六步：ICP精配准。

接下来，我们简单介绍下各过程，如有不当之处，还请留言批评指正。

对于第一步：加载点云。

demo中给出了两种点云的格式的读取（ply和pcd格式），当然在PCL中，还有其它数据格式的读取函数封装，比如txt，以及二进制数据格式的读取。

对于第二步：关于下采样滤波。

可以参考笔者之前写过的一篇文章：《PCL从0到1|点云滤波之直通滤波与体素法滤波》，此处不再赘言。

对于第三步：计算表面法线。

表面法线是几何表面的重要属性，在很多领域都有大量应用，比如：在进行光照渲染时产生符合可视习惯时需要表面法线信息才能正常表达，对于一个已知的几何体表面，根据垂直于点表面的矢量，因此推断表面某一点的法线方向通常比较简单。然而，由于我们获取的点云数据集在真实物体的表面表现为一组定点样本，这样通常就会有两种解决办法：

（1）使用曲面重建技术，从获取的点云数据集中得到采样点对应的曲面，然后从曲面模型中计算表面法线。

（2）直接从点云数据集中近似推断表面法线。

此处我们简单介绍下对于已知一个点云数据集，如何在每个点处直接近似计算表面法线。

方法简单表述如下：确定表面一点法线的问题近似于估计表面的一个相切面法线的问题，因此转换过来以后就变成一个最小二乘法平面拟合估计问题。因此，估计表面法线的解决方案就变成了分析一个协方差矩阵的特征矢量和特征值（或者PCA——主成分分析），这个协方差矩阵从查询点的近邻元素中创建。

在PCL内估计一个点集对应的协方差矩阵，可以使用以下函数调用实现：

//定义每个表面小块的3×3协方差矩阵的存储对象

Eigen::Matrix3f covariance_matrix;

//定义一个表面小块的质心坐标16字节对齐存储对象

Eigen::Vector4f xyz_centroid;

//估计质心坐标

Compute3DCentroid(cloud,xyz_centroid);

//计算3×3协方差矩阵

computeCovarianceMatrix(cloud,xyz_centroid,covariance_matrix);

对于法线的正负向如何确定问题，此处留给读者思考。

对于第四步：计算FPFH。

已知点云P中有n个点，那么它的点特征直方图（PFH）的理论计算复杂度是O(nk2),其中k是点云P中每个点p计算特征向量时考虑的邻域数量。对于实时应用或接近实时应用中，密集点云的点特征直方图（PFH）的计算，是一个主要的性能瓶颈。

此处简单介绍下FPFH（快速点特征信息）与PFH(点特征直方图)的主要区别。

（1）FPFH没有对全互联Pq点的所有邻近点的计算参数进行统计，因此可能会漏掉了一些重要的点对，而这些漏掉的点对可能对捕获查询点周围的几何特征有贡献。

（2）PFH特征模型是在查询点周围的一个精确的邻域半径内，而FPFH还包括半径r范围以外的额外点对（不过在2r内）。

第五步：SAC_IA粗配准

对于初始的变换矩阵粗略估计，贪婪的初始配准方法工作量很大，它使用了点云数据旋转不变的特性。但计算复杂度较高，因此在合并的步骤需要查看所有可能的对应关系。此外，因为这是一个贪婪算法，所以有可能只能得到局部最优解。

因此我们采用采样一致性方法，试图保持相同的对应关系而不必尝试了解有限个对应关系的所有组合。相反，我们从候选对应关系中进行大量的采样并通过以下的步骤对它们中的每一个进行排名。

（1）从点云P中选择n个样本点，为了尽量保证所采样的点具有不同的FPFH特征，确定他们的配对距离大于用户设定的最小值dmin；

（2）对于每个样本点，在点云Q中找到满足FPFH相似的点存入一个列表中。从这些点中随机选择一些代表采样点的对应关系；

（3）计算通过采样点定义的刚体变换和其对应变换，计算点云的度量错误来评价转换的质量；

重复上述的三个步骤，直至取得储存了最佳度量错误，并使用暴力配准部分数据。最后使用Levenberg-Marquardt算法进行非线性局部优化。

第六步：迭代最近点算法（ICP精配准）

我们先来观察一下PCL1.8中封装了ICP的函数实现，此处附上ICP的核心函数实现源码：

///////////////////////////////////////////////////////////////////////////////////////////

template void

pcl::IterativeClosestPoint::computeTransformation (

PointCloudSource &output, const Matrix4 &guess)

{

// Point cloud containing the correspondences of each point in

PointCloudSourcePtr input_transformed (new PointCloudSource);

nr_iterations_ = 0;

converged_ = false;

// Initialise final transformation to the guessed one

final_transformation_ = guess;

// If the guessed transformation is non identity

if (guess != Matrix4::Identity ())

{

input_transformed->resize (input_->size ());

// Apply guessed transformation prior to search for neighbours

transformCloud (*input_, *input_transformed, guess);

}

else

*input_transformed = *input_;

transformation_ = Matrix4::Identity ();

// Make blobs if necessary

determineRequiredBlobData ();

PCLPointCloud2::Ptr target_blob (new PCLPointCloud2);

if (need_target_blob_)

pcl::toPCLPointCloud2 (*target_, *target_blob);

// Pass in the default target for the Correspondence Estimation/Rejection code

correspondence_estimation_->setInputTarget (target_);

if (correspondence_estimation_->requiresTargetNormals ())

correspondence_estimation_->setTargetNormals (target_blob);

// Correspondence Rejectors need a binary blob

for (size_t i = 0; i < correspondence_rejectors_.size (); ++i)

{

registration::CorrespondenceRejector::Ptr& rej = correspondence_rejectors_[i];

if (rej->requiresTargetPoints ())

rej->setTargetPoints (target_blob);

if (rej->requiresTargetNormals () && target_has_normals_)

rej->setTargetNormals (target_blob);

}

convergence_criteria_->setMaximumIterations (max_iterations_);

convergence_criteria_->setRelativeMSE (euclidean_fitness_epsilon_);

convergence_criteria_->setTranslationThreshold (transformation_epsilon_);

if (transformation_rotation_epsilon_ > 0)

convergence_criteria_->setRotationThreshold (transformation_rotation_epsilon_);

else

convergence_criteria_->setRotationThreshold (1.0 – transformation_epsilon_);

// Repeat until convergence

do

{

// Get blob data if needed

PCLPointCloud2::Ptr input_transformed_blob;

if (need_source_blob_)

{

input_transformed_blob.reset (new PCLPointCloud2);

toPCLPointCloud2 (*input_transformed, *input_transformed_blob);

}

// Save the previously estimated transformation

previous_transformation_ = transformation_;

// Set the source each iteration, to ensure the dirty flag is updated

correspondence_estimation_->setInputSource (input_transformed);

if (correspondence_estimation_->requiresSourceNormals ())

correspondence_estimation_->setSourceNormals (input_transformed_blob);

// Estimate correspondences

if (use_reciprocal_correspondence_)

correspondence_estimation_->determineReciprocalCorrespondences (*correspondences_, corr_dist_threshold_);

else

correspondence_estimation_->determineCorrespondences (*correspondences_, corr_dist_threshold_);

//if (correspondence_rejectors_.empty ())

CorrespondencesPtr temp_correspondences (new Correspondences (*correspondences_));

for (size_t i = 0; i < correspondence_rejectors_.size (); ++i)

{

registration::CorrespondenceRejector::Ptr& rej = correspondence_rejectors_[i];

PCL_DEBUG (“Applying a correspondence rejector method: %s.\n”, rej->getClassName ().c_str ());

if (rej->requiresSourcePoints ())

rej->setSourcePoints (input_transformed_blob);

if (rej->requiresSourceNormals () && source_has_normals_)

rej->setSourceNormals (input_transformed_blob);

rej->setInputCorrespondences (temp_correspondences);

rej->getCorrespondences (*correspondences_);

// Modify input for the next iteration

if (i < correspondence_rejectors_.size () – 1)

*temp_correspondences = *correspondences_;

}

size_t cnt = correspondences_->size ();

// Check whether we have enough correspondences

if (static_cast (cnt) < min_number_correspondences_)

{

PCL_ERROR (“[pcl::%s::computeTransformation] Not enough correspondences found. Relax your threshold parameters.\n”, getClassName ().c_str ());

convergence_criteria_->setConvergenceState(pcl::registration::DefaultConvergenceCriteria::CONVERGENCE_CRITERIA_NO_CORRESPONDENCES);

converged_ = false;

break;

}

// Estimate the transform

transformation_estimation_->estimateRigidTransformation (*input_transformed, *target_, *correspondences_, transformation_);

// Transform the data

transformCloud (*input_transformed, *input_transformed, transformation_);

// Obtain the final transformation

final_transformation_ = transformation_ * final_transformation_;

++nr_iterations_;

// Update the vizualization of icp convergence

//if (update_visualizer_ != 0)

// update_visualizer_(output, source_indices_good, *target_, target_indices_good );

converged_ = static_cast((*convergence_criteria_));

}

while (convergence_criteria_->getConvergenceState() == pcl::registration::DefaultConvergenceCriteria::CONVERGENCE_CRITERIA_NOT_CONVERGED);

// Transform the input cloud using the final transformation

PCL_DEBUG (“Transformation is:\n\t%5f\t%5f\t%5f\t%5f\n\t%5f\t%5f\t%5f\t%5f\n\t%5f\t%5f\t%5f\t%5f\n\t%5f\t%5f\t%5f\t%5f\n”,

final_transformation_ (0, 0), final_transformation_ (0, 1), final_transformation_ (0, 2), final_transformation_ (0, 3),

final_transformation_ (1, 0), final_transformation_ (1, 1), final_transformation_ (1, 2), final_transformation_ (1, 3),

final_transformation_ (2, 0), final_transformation_ (2, 1), final_transformation_ (2, 2), final_transformation_ (2, 3),

final_transformation_ (3, 0), final_transformation_ (3, 1), final_transformation_ (3, 2), final_transformation_ (3, 3));

// Copy all the values

output = *input_;

// Transform the XYZ + normals

transformCloud (*input_, output, final_transformation_);

}

在PCL中，IterativeClosestPoint类提供了标准ICP算法的实现（The transformation is estimation based on SVD），其大致思路如下：

（1）将初始配准后的两片点云P’（经过坐标变换后的源点云）和点云Q,作为精配准的初始点集；

（2）对源点云P’中的每一点Pi，在目标点云Q中寻找距离最近的对应点Qi，作为该点在目标点云中的对应点，组成初始对应点对；

（3）初始对应点集中的对应关系并不一定都是正确的，错误的对应关系会影响最终的配准结果，采用方向向量阈值提剔除错误的对应点对；

（4）计算旋转矩阵R和平移向量T，使对应点集之间的均方误差最小；

（5）设定某一阈值E和最大迭代次数N,将上一步得到的刚体变换作用于源点云P’，得到新点云P’’，计算P’’和Q的距离误差，如果两次迭代的误差小于阈值E或者当前的迭代次数大于N，则迭代结束，否则将初始配准的点集更新为P’’和Q,继续重复上述步骤，直至满足收敛条件。

ICP算法对于参数较为敏感，此处简单介绍一下每个参数的含义：

1、setMaximumIterations 设置最大迭代次数，ICP算法最多迭代的次数。

2、setEuclideanFitnessEpsilon设置收敛条件是均方误差和小于阈值，停止迭代。

3、setMaxCorrespondenceDistance设置对应点对之间的最大距离（影响因素较大）。

4、setTransformationEpsilon 设置两次变换矩阵之间的差值（一般设置为1e-10）。

主要参考:

1、郭浩主编的<点云库PCL从入门到精通>

2、参考博文：

https://blog.csdn.net/peach_blossom/article/details/78506184

上述内容，如有侵犯版权，请联系作者，会自行删文。