ThreeJS简易魔方自动还原实现

© Young 2018-04-29 21:08

Welcome to My GitHub

在ThreeJS四步制作一个简易魔方中介绍了怎么实现一个可以转动的简易魔方，接来下准备介绍下怎么让这个简易魔方具备自动还原的功能。

例子如下：

可以扫描以下二维码体验：

https://newbieyoung.github.io/Threejs_rubik/step5.html (二维码自动识别)

或者访问链接https://newbieyoung.github.io/Threejs_rubik/step5.html；

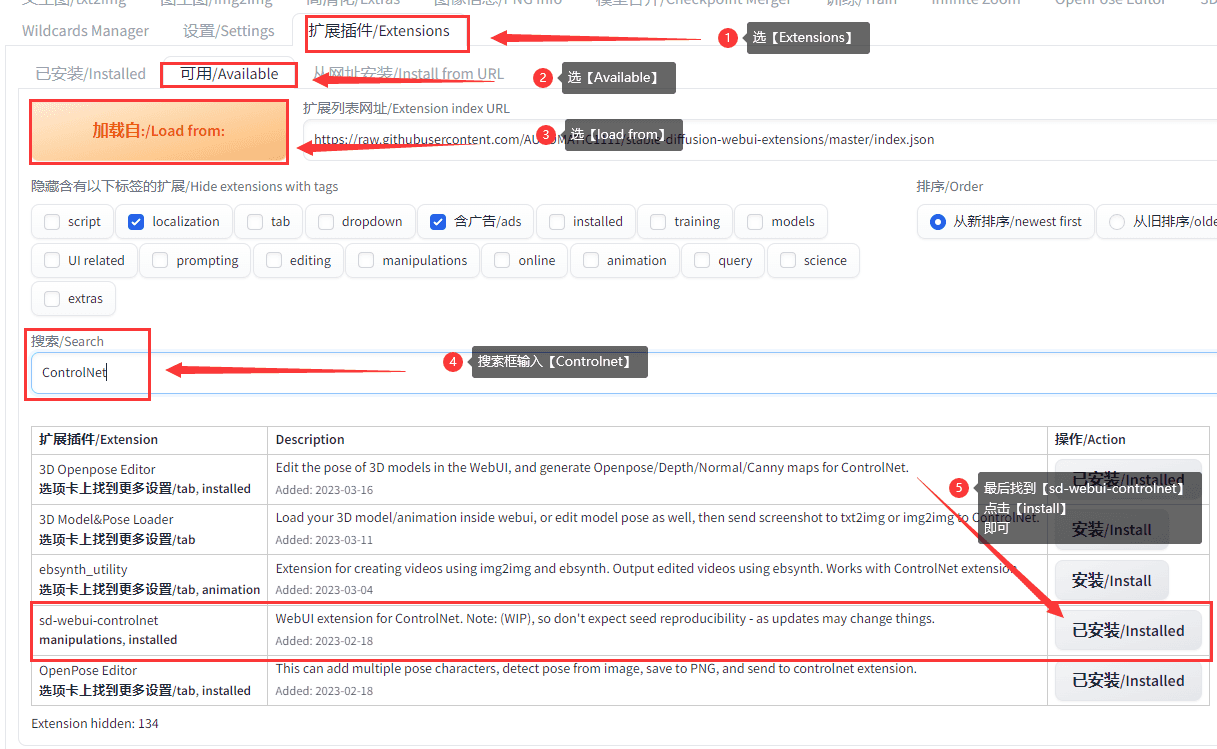
代码在https://github.com/newbieYoung/Threejs_rubik项目中：

step1.html、step2.html、step3.html、step4.html为ThreeJS四步制作一个简易魔方的相关代码；

wegame文件夹为简易魔方的小游戏代码，目前只包含前四步功能；

step5.html为简易魔方层先法自动还原的代码，也就是上述例子的代码，后续会进行简单说明；

auto-reset-v1-test.js为上述例子的测试用例代码，在测试用例中会把相关日志信息（比如还原所需步数以及时长）输出到auto-reset-v1-log.txt文件中，方便后续分析；

analyze.js为上述例子的日志分析代码，会计算所有样本数据的平均时长和平均步数并把结果输出到auto-reset-v1-analyze.txt文件中。

在210次自动测试中，平均步数为197步，平均时长为44秒，和代码中设定的0.2秒一步基本吻合，从自动测试数据来看，目前的实现还没有达到该算法的最优，估计可以优化到平均步数150的样子（旋转90度即算一步）。

需要注意的是三阶魔方有8!×3^7×12!×2^11/2 = 43252003274489856000种情形，因此虽然我对例子代码进行了上千测试，但是依然不能百分百保证实现的还原算法可以处理所有情况，因此希望大家在体验的过程中如果遇到的异常情况能反馈给我（最好是六个面都截图）。

层先法是指将魔方分为三层：底层、中层、顶层，分层复原；仔细留意上述例子就可以发现复原过程是从底层开始慢慢到顶层的，如图：

层先法只需要记忆几个简单的公式就可以完成，因此适合魔方初学者使用，但是效率较差。

该怎么实现呢？以第一步小白花来说：

首先得确定当前模型中上表面中心颜色的对应颜色；

小白花要求上表面中心颜色四周为其对应颜色；

所幸我们在ThreeJS中根据颜色数组构建正方体时其规律就已经确定了；

当我们依次给六个面赋值时，其固定顺序为右、左、上、下、前、后，也就意味着根据颜色序号获取初始化时其对面颜色序号的方法如下：

这是层先法实现过程中的第一个基本方法。

因为魔方转动时使用的是ThreeJS提供轨道控制器OrbitControls，视角变动的原因在于摄像机位置的变化，魔方本身并没有转动；再加上转动某一层之后会更新小方块序号，使其永远保持初始序号不变；

那么上表面中心小方块序号则为10，与此同时我们需要一个方法来根据序号选取小方块：

rotateNum表示小方块绕世界坐标系的Y轴旋转逆时针旋转90度的次数，比如getCubeByIndex(2,1)实际获取的小方块序号为20；

之所以会这样是因为层先法中每一种情况实际还有三个等效的情形，因为魔方的上下关系确定后就固定了，但是左右前后却是可以变化的；

这是层先法实现过程中的第二个基本方法。

选取到具体小方块之后我们还需要获得小方块中法向量和世界坐标系Y轴平行的平面的序号然后根据该平面的序号获取对应颜色，因此我们还需要一个方法来获取某个小方块中法向量和已知向量方向相同的面的颜色序号：

这个方法里边需要注意两点：

其一：判断两个向量平行时不能判断其夹角是否等于0，因为浮点数运算存在误差，实际情况可能是其夹角是个很小很小的数但是就是不等于0，得改成判断最小值的方法；

其二：cube.faces[i].normal获取的法向量是在小方块自身坐标系中的，所幸ThreeJS需要进行光线相关的运算，因此小方块对象中存储了法向量矩阵cube.normalMatrix，自身坐标系的法向量乘以法向量矩阵即可得到视图坐标系中的法向量；但是因为我们传入这个方法的坐标轴向量在世界坐标系中，因此不能拿来直接计算，需要转换到视图坐标系中去，转换方法就是乘以视图矩阵的逆反矩阵；

因为使用的是透视投影相机 THREE.PerspectiveCamera因此视图矩阵可以这么求：

直接调用THREE.Matrix4的静态方法getInverse即可求得某个矩阵的逆反矩阵；

这是层先法实现过程中的第三个基本方法。

到此我们就可以实现首先得确定当前模型中上表面中心颜色的对应颜色这一步骤了：

然后判断小白花是否完成，如果完成则进入第二步；

小白花的判断很简单，只需要判断序号为1、9、11、19的小方块的上表面颜色是否为中心小方块上表面颜色的对应色即可：

然后得处理小白花的各种情况；

以第一种举例来说：

如图3号小方块Z轴表面为底色时，如果9号小方块Y轴表面也为底色，则需要逆时针转动顶层；反之则需要逆时针转动左侧：

上述代码有两个需要注意的地方：

其一：rotateAxisByYLine方法是用于处理各种等效情况中各坐标轴的变化情况的，比如Z轴在逆时针绕Y轴旋转90度之后就变成了X轴；

这是层先法实现过程中的第四个基本方法。

其二：逆时针转动顶层的逻辑被u方法所封装；逆时针转动左侧的逻辑被l方法所封装；原因在于层先法还原魔方的各种转动最终都可以被封装为12基本转动，如下：

在代码中分别封装如下：

这是层先法实现过程中的其它基本方法了。

后续按照教程一步步实现即可，基本都是上述基本方法的应用了。

层先法虽然理解起来简单，但是因为步骤较多，实现起来容易出错，写代码的时候最好仔细点！

另外想做一个基于微信小游戏的魔方，前期主要想复刻好魔方体验并结合一些方便的小功能比如标记某一状态，后续操作有问题立刻回归标记状态，以及操作历史，信息统计等；欢迎有兴趣的同学一起来玩（在我博客留言留下联系方式即可）。

最后是广告时间……