1.闵可夫斯基距离:计算用户相似度
闵可夫斯基距离可以概括曼哈顿距离与欧几里得距离。
其中r越大,单个维度差值大小会对整体产生更大的影响。这个很好理解,假设当r=2时一个正方形对角线长度,永远是r=3时正方体对角线的投影,因此r越大,单个维度差异会有更大影响。(所以这也可能是很多公司的推荐算法并不准确的原因之一)
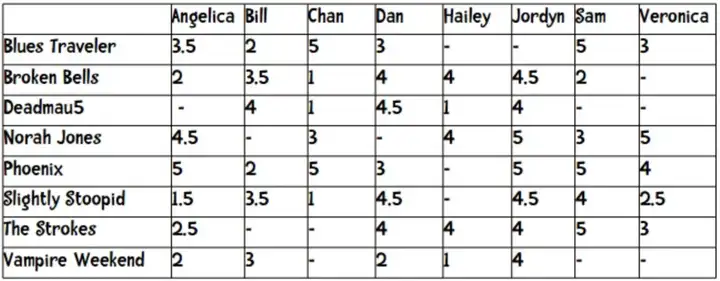
我们在对一个新用户进行推荐时,可以计算在同等维度下其他用户的闵可夫斯基距离。这种海量数据的二维表格,用pandas处理十分方便
下面有一个闵可夫距离计算的实例
from math import sqrt
users = {“Angelica”: {“Blues Traveler”: 3.5, “Broken Bells”: 2.0, “Norah Jones”: 4.5, “Phoenix”: 5.0, “Slightly Stoopid”: 1.5, “The Strokes”: 2.5, “Vampire Weekend”: 2.0},
“Bill”:{“Blues Traveler”: 2.0, “Broken Bells”: 3.5, “Deadmau5”: 4.0, “Phoenix”: 2.0, “Slightly Stoopid”: 3.5, “Vampire Weekend”: 3.0},
“Chan”: {“Blues Traveler”: 5.0, “Broken Bells”: 1.0, “Deadmau5”: 1.0, “Norah Jones”: 3.0, “Phoenix”: 5, “Slightly Stoopid”: 1.0},
“Dan”: {“Blues Traveler”: 3.0, “Broken Bells”: 4.0, “Deadmau5”: 4.5, “Phoenix”: 3.0, “Slightly Stoopid”: 4.5, “The Strokes”: 4.0, “Vampire Weekend”: 2.0},
“Hailey”: {“Broken Bells”: 4.0, “Deadmau5”: 1.0, “Norah Jones”: 4.0, “The Strokes”: 4.0, “Vampire Weekend”: 1.0},
“Jordyn”: {“Broken Bells”: 4.5, “Deadmau5”: 4.0, “Norah Jones”: 5.0, “Phoenix”: 5.0, “Slightly Stoopid”: 4.5, “The Strokes”: 4.0, “Vampire Weekend”: 4.0},
“Sam”: {“Blues Traveler”: 5.0, “Broken Bells”: 2.0, “Norah Jones”: 3.0, “Phoenix”: 5.0, “Slightly Stoopid”: 4.0, “The Strokes”: 5.0},
“Veronica”: {“Blues Traveler”: 3.0, “Norah Jones”: 5.0, “Phoenix”: 4.0, “Slightly Stoopid”: 2.5, “The Strokes”: 3.0}
}
def minkefu(rating1, rating2, n):
“””Computes the Manhattan distance. Both rating1 and rating2 are dictionaries
of the form {The Strokes: 3.0, Slightly Stoopid: 2.5}”””
distance = 0
commonRatings = False
for key in rating1:
if key in rating2:
distance += abs((rating1[key] – rating2[key])**n)
commonRatings = True
if commonRatings:
return distance**1/n
else:
return –1 #Indicates no ratings in common def computeNearestNeighbor(username, users):
“””creates a sorted list of users based on their distance to username”””
distances = []
for user in users:
if user != username:
distance = minkefu(users[user], users[username], 2)
distances.append((distance, user))
# sort based on distance — closest first distances.sort()
return distances
def recommend(username, users):
“””Give list of recommendations””” # first find nearest neighbor
nearest = computeNearestNeighbor(username, users)[0][1]
recommendations = []
# now find bands neighbor rated that user didnt
neighborRatings = users[nearest]
userRatings = users[username]
for artist in neighborRatings:
if not artist in userRatings:
recommendations.append((artist, neighborRatings[artist]))
# using the fn sorted for variety – sort is more efficient return sorted(recommendations, key=lambda artistTuple: artistTuple[1], reverse = True)
# examples – uncomment to run print( recommend(Hailey, users))
2.皮尔逊相关系数:如何解决主观评价差异带来的推荐误差
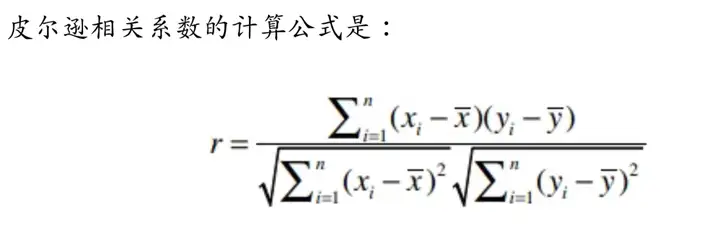
在第一部分提到r越大,单个维度差值大小会对整体产生更大的影响。因此,我们需要有一个解决方案来应对个体的主观评价差异。这个东西就是皮尔逊相关系数。
上述公式计算复杂度很大,需要进行n!*m!次遍历,后续有一个近似计算公式可以大大降低算法复杂度。
皮尔逊相关系数(-1,1)用于衡量两个向量(用户)的相关性,如两个用户意见基本一致,那皮尔逊相关系数靠近1,如果两个用户意见基本相反,那皮尔逊相关系数结果靠近-1。在这里,我们需要弄明白两个问题:
(1)怎么确定多维向量之间的皮尔逊相关系数
(2)怎么利用闵可夫斯基距离结合起来,优化我们的推荐模型
对第(1)问题,在这里有一个近似计算公式
用代码来表示则为
def pearson(rating1, rating2):
sum_xy = 0
sum_x = 0
sum_y = 0
sum_x2 = 0
sum_y2 = 0
n = 0
for key in rating1:
if key in rating2:
n += 1
x = rating1[key]
y = rating2[key]
sum_xy += x * y
sum_x += x
sum_y += y
sum_x2 += pow(x, 2)
sum_y2 += pow(y, 2)
# now compute denominator
denominator = sqrt(sum_x2 – pow(sum_x, 2) / n) * sqrt(sum_y2 – pow(sum_y, 2) / n)
if denominator == 0:
return 0
else:
return (sum_xy – (sum_x * sum_y) / n) / denominator
(2)对于问题2,假设一个场景:
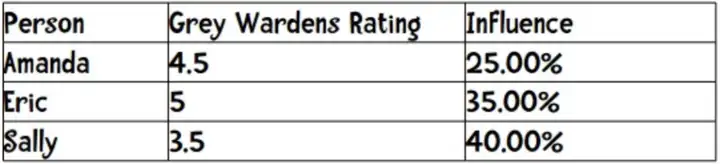
现在Anne需要听一首歌,从相似的三个相似用户中可以看出他们的皮尔逊系数为:
三个人对这首歌的推荐均有贡献,那我们怎么确认比重呢?由于0.8+0.7+0.5=2,因此可以按1的百分比取,则
因此,这首歌的最后得分是4.5*0.25+5*0.35+3.5*0.4=4.275
这样计算的好处是将多个用户推荐权重整合起来,这样不会因为单一用户的个人喜好或者经历导致推荐失误。这也是接下来要说的K临近算法。
3.稀疏矩阵的处理办法:余弦相似度
如果数据是密集的,则用闵可夫斯基距离来计算距离;
如果数据是稀疏的,则使用余弦相似度来计算相似度(-1,1)
4.避免个人因素而生成的错误推荐:K临近算法
见2中的例子(2)
python已有现成的KNN算法库,本质是找到跟目标最近距离的几个点,详情可以参考:http://python.jobbole.com/83794/

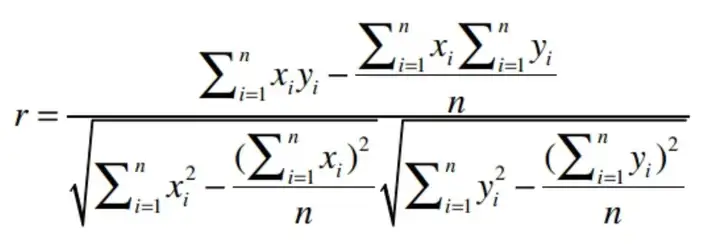
















暂无评论内容