基本原理
核心思想
每次排序都会选一个基准数,小于基准数的放在左子序列,大于等于基准数的放在右子序列。
原始序列:{13, 15, 8, 54, 23}
step1:随机选一个基准数15,则其左子序列{13, 8},右子序列{54, 23}
step2.1:序列{13, 8}随机选一个基准数8,则其左子序列{},右子序列{13}
step2.2:序列{54, 23}随机选一个基准数23,则其左子序列{},右子序列{54}
当子序列包含的元素个数小于等于1时停止循环,排序工作已经完成
编码思路
1、如何将待排序序列重新组合成“左子序列 + 基准数 + 右子序列”?
随机从待排序序列中选一个基准数,然后 for 循环遍历待排序序列,如果当前元素的值小于基准数,就将该元素放在左子序列。那究竟是放在左子序列的哪个位置上?这肯定涉及到元素交换,所以要维护一个索引 i,如果当前元素的值小于基准数,就和索引 i 位置上的元素互换位置。
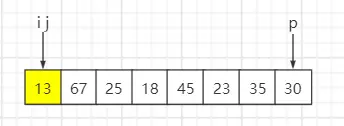
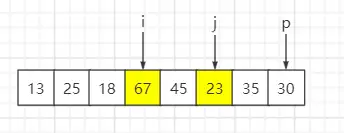
待排序序列:{13, 67, 25, 18, 45, 23, 35, 30},固定选最后一个元素即30为基准数,索引 i 初始值为0,索引 j 为 for 循环遍历当前元素所在的索引。
step1:遍历第一个元素13,比基准数30小,与索引 i 元素互换位置,然后 i++、j++
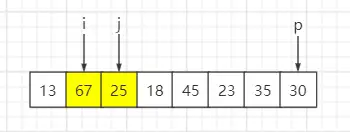
step2:遍历第二个元素67,比基准数30大,i 保持不变、j++
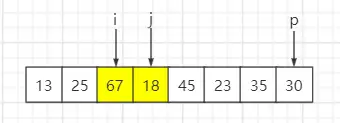
step3:遍历第三个元素25,比基准数30小,与索引 i 元素互换位置,然后 i++、j++
step4:遍历第四个元素18,比基准数30小,与索引 i 元素互换位置,然后 i++、j++
step5:遍历第五个元素45,比基准数30大,i 保持不变、j++
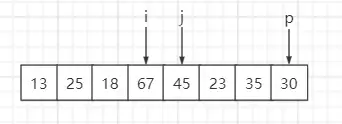
step6:遍历第六个元素23,比基准数30小,与索引 i 元素互换位置,然后 i++、j++
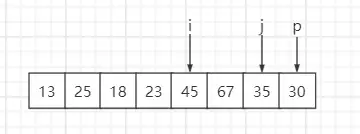
step7:遍历第七个元素35,比基准数30大,i 保持不变、j++
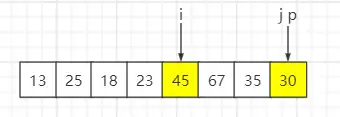
step8:遍历到基准数时,p 与 i 元素互换
最终结果:索引 i 元素值为30,左子序列小于基准数30,右子序列大于等于基准数30。
序列{13, 15, 8, 54, 23, 25, 17, 11, 78, 89, 67, 56, 54, 34, 97, 15}经过第一轮排序后就变成
{13, 8, 11, 15, 23, 25, 17, 15, 78, 89, 67, 56, 54, 34, 97, 54},其中基准数15所在的索引是3。
比基准数15(索引为3)小的都在左子序列,符合预期。
package main
import “fmt”
func main() {
data := []int{13, 15, 8, 54, 23, 25, 17, 11, 78, 89, 67, 56, 54, 34, 97, 15}
fmt.Printf(“before sort:%v\n”, data)
sort(data)
// after sort:[13 8 11 15 23 25 17 15 78 89 67 56 54 34 97 54]
fmt.Printf(“after sort:%v\n”, data)
}
func sort(data []int) {
if len(data) <= 1 {
return
}
i := 0
for j := 0; j <= len(data)–1; j++ {
if data[j] < data[len(data)–1] {
temp := data[i]
data[i] = data[j]
data[j] = temp
i++
}
}
temp := data[len(data)–1]
data[len(data)–1] = data[i]
data[i] = temp
// i value:3
fmt.Printf(“i value:%v\n”, i)
}
2、代码实现中固定选最后一个元素为基准数,那如何实现随机选一个元素为基准数?
思路:rand.Seed 在 “0-len(data)-1”之间随机产生一个值,然后将该位置上的元素和最后一个元素交换位置。
package main
import (
“fmt”
“math/rand”
“time”
)
func main() {
data := []int{13, 15, 8, 54, 23, 25, 17, 11, 78, 89, 67, 56, 54, 34, 97, 15}
fmt.Printf(“before sort:%v\n”, data)
random(data)
sort(data)
// after sort:[13 15 8 15 23 25 17 11 34 54 67 56 54 78 97 89]
fmt.Printf(“after sort:%v\n”, data)
}
func sort(data []int) {
if len(data) <= 1 {
return
}
i := 0
for j := 0; j <= len(data)–1; j++ {
if data[j] < data[len(data)–1] {
temp := data[i]
data[i] = data[j]
data[j] = temp
i++
}
}
temp := data[len(data)–1]
data[len(data)–1] = data[i]
data[i] = temp
// i value:9
fmt.Printf(“i value:%v\n”, i)
}
func random(data []int) {
rand.Seed(time.Now().UnixNano())
p := rand.Intn(len(data) – 1)
fmt.Printf(“random value:%v\n”, p)
temp := data[len(data)–1]
data[len(data)–1] = data[p]
data[p] = temp
}
代码实现
package main
import (
“fmt”
“math/rand”
“time”
)
func main() {
data := []int{13, 15, 8, 54, 23, 25, 17, 11, 78, 89, 67, 56, 54, 34, 97, 15}
fmt.Printf(“before sort:%v\n”, data)
quickSort(data, 0, len(data)–1)
fmt.Printf(“after sort:%v\n”, data)
}
func randomizedPartition(data []int, low, high int) int {
rand.Seed(time.Now().UnixNano())
p := rand.Intn(high–low) + low
temp := data[high]
data[high] = data[p]
data[p] = temp
return partition(data, low, high)
}
func partition(data []int, low, high int) int {
pivot := data[high]
i := low
for j := low; j < high; j++ {
if data[j] <= pivot {
temp := data[i]
data[i] = data[j]
data[j] = temp
i++
}
}
data[high] = data[i]
data[i] = pivot
return i
}
func quickSort(data []int, low, high int) {
if high > low {
p := randomizedPartition(data, low, high)
// quickSort(data, low, p) incorrect, will cause stack overflow
quickSort(data, low, p–1)
quickSort(data, p+1, high)
}
}
时间复杂度
平均时间复杂度:O( nlog2nnlog_{2}n )
最好时间复杂度:O( nlog2nnlog_{2}n )
最坏时间复杂度:O( n2n^{2} ),选的基准数只能将序列分为一个元素与其他元素两部分,这时的快速排序退化为冒泡排序
最坏时间复杂度
(1)分区函数每次选取的基准数为序列最小元素。
(2)分区函数每次选取的基准数为序列最大元素。
具体案例:序列已经正序或逆序排好,选的基准数每次都是序列第一个元素或最后一个元素。
稳定性
排序算法的稳定性概念
大小相同的两个值在排序之前和排序之后的先后顺序不变
序列{13, 67, 25, 67,18},排序之后能保证原序列第一个67一定在原序列第二个67的前面,就是稳定的排序算法。
排序算法稳定性的作用
A{V1:500, V2:300}、B{V1:400, V2:300}、C{V1:300, V2:200}
需求:先按V1降序排序,再按V2降序排序
预期排序结果:A{V1:500, V2:300}、B{V1:400, V2:300}、C{V1:300, V2:200}
使用快速排序算法进行排序(先说结论,快速排序是不稳定的)
先按V1降序排序:A{V1:500, V2:300}、B{V1:400, V2:300}、C{V1:300, V2:200}
再按V2降序排序,有两种可能结果,因为A和B的V2值相等。
第一种:A{V1:500, V2:300}、B{V1:400, V2:300}、C{V1:300, V2:200}
第二种:B{V1:400, V2:300}、A{V1:500, V2:300}、C{V1:300, V2:200}
快速排序算法是不稳定的
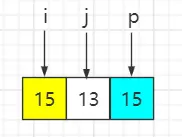
待排序序列:{15, 13, 15},选最后一个元素即15为基准数,索引 i 初始值为0,索引 j 为 for 循环遍历当前元素所在的索引。
step1:遍历第一个元素15,大于等于基准数15,i 保持不变、j++
step2:遍历第一个元素13,比基准数15小,与索引 i 元素互换位置,然后 i++、j++
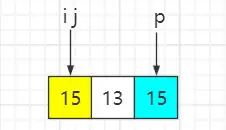
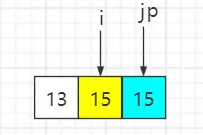
step3:遍历到基准数时,p 与 i 元素互换
最终结果:大小相同的两个元素15在排序之前和排序之后的先后顺序已经发生变化


















暂无评论内容