0.背景
因子分解机(FM, Factorization Machines)是推荐领域应用最为广泛的模型之一,在前深度学习时代,其凭借着良好的特征组合(表达)能力一度取代了协同过滤(CF, Collaborative Filtering)、逻辑回归(LR, Logistic Regression )的主流模型地位。而在深度学习牢牢占据着主流的今天,FM仍旧可以为深度模型提供优化思路。
接下来,就让我们来了解一下FM的算法原理,以及其相对CF、LR的长处所在。
1.协同过滤
在介绍FM之前,我们先简要回顾一下曾经的主流模型协同过滤和逻辑回归。
虽然现在不属于协同过滤推荐的天下,但是如果论资排辈、论影响力和应用范围,协同过滤类算法恐怕会被排为首位。可作为解释的原因有一下几点:
应用早;可解释性强;易于实现;推荐思想仍不过时;在某些场景下使用效果仍旧良好;在商业应用上,协同顾过滤可以追溯到1992年,当时Xerox公司基于其开发了一个邮件推送服务Tapestry。所以在资历上协同过滤绝对算绝对的老资格了,要知道1992年的互联网还处于萌芽期,博纳斯-李的万维网发布才一年。而在2003年,现在的电子商务巨头、彼时的电子商务先锋Amazon 便以论文Amazon.com recommendations item-to-item collaborative这一论文展示其主推荐系统基于协同过滤类算法构建。而后有着Amazon等大厂的“背书”,协同过滤在很长的一段时间中是业界的研究热点和主流。
1.1协同过滤算法的原理
协同过滤算法的原理非常朴素,其基于物以类聚、人以群分的常识理念,认为相似人群拥有相似的兴趣爱好、相似的物品可以推荐给同一类人。
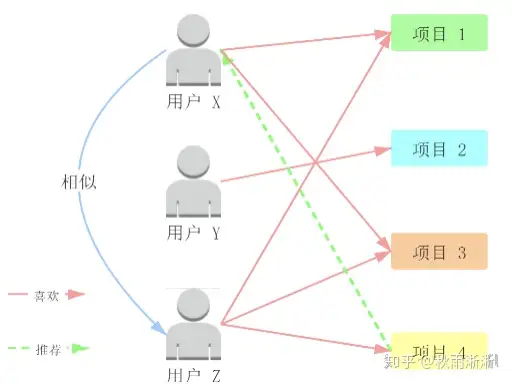
在实现步骤上也很简单直观(以UserCF为例,ItemCF类似),如下图所示:
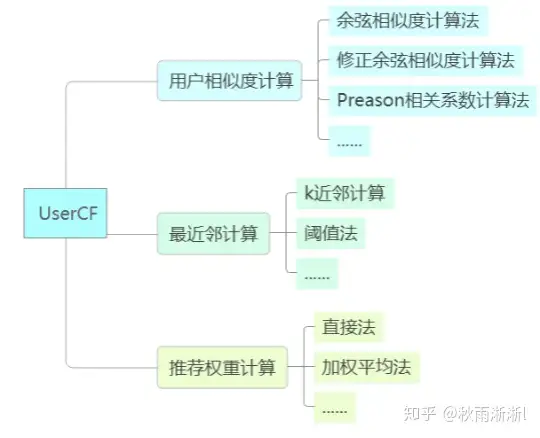
在计算上,能称得上复杂的可能只有用户相似度计算这一部分了。不过也只是做一个 将用户评价矩阵转为了用户相似度矩阵的操作,同时在相似度计算上,也是采用这种很基础的余弦相似度类计算法。
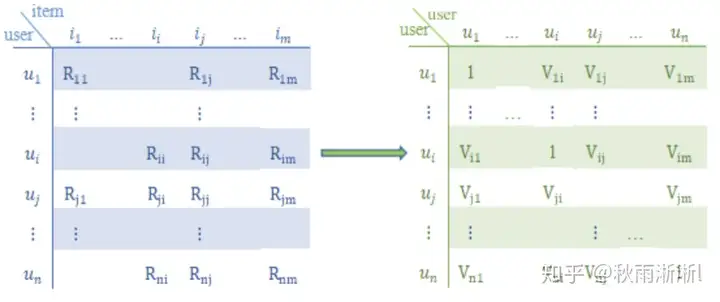
大概给两个公式意思一下:
simuv=cos(u,v)=u.v|u||v|=∑i∈Iuvrui×rvi∑i∈Iurui2∑i∈Ivrvi2sim_{uv}=cos(u,v)=\frac{u.v}{|u||v|} = \frac{\sum_{i \in I_{uv}} r_{ui} \times r_{vi}} { \sqrt{\sum_{i \in I_u} r_{ui}^2 } \sqrt{\sum_{i \in I_v} r_{vi}^2 } }\\rui^=r¯u+∑v∈Ni(u)simuv×(rvi−r¯v)∑v∈Ni(u)simuv\hat{r_{ui}} = \bar{r}_u + \frac{\sum_{v \in N_i(u) \ sim_{uv} \times(r_{vi} – \bar{r}_v) }} { \sum_{v \in N_i(u)} \ sim_{uv}}\\
从上文的描述可以看出,协同过滤类算法的原理和实现可谓十分简便,它不需要设损失函数、梯度下降求最优解这些现在模型训练常规操作。另外所要求的数据也非常简约(只需要用户的对商品的评分数据),但也正是因为这些问题,协同过滤类算法存在着以下缺点:
表达能力不强;
只用了用户的评分数据这一特征,且不能在模型中加入其它特征(如用户年龄、性别、商品属性等)进行训练来增加模型的表达能力,这极大了限制了模型的上限。较难准确的找到相似用户;
在互联网应用的场景下,用户的历史数据相对于总商品数而言总数极度的稀疏,导致协同类算法不适用于获取用户评分数据较为困难的场景。存在冷启动问题;
对于新用户、新商品,由于极度缺乏,很难保证推荐质量。需要维护一张巨大的用户相似度矩阵/商品相似度矩阵。2.逻辑回归模型
逻辑回归本质上是个分类模型,相较于协同过滤类算法利用用户和物品的相似度进行推荐,逻辑回归是将推荐问题转化为一个分类问题来解决或者说是一个点击率预估(Click Through Rate , CTR)问题。
在特征的使用上,逻辑回归可以综合用户、物品、时间上下文等多种维度的信息进行模型训练,不再局限于单一维度的评分信息,从而来增强模型的表达和泛化能力,这是其优于协同过滤类算法最显著的特点。
逻辑回归模型的其它优点如下:
数学上符合CTR预估物理含义;
逻辑回归与CTR预估模型的因变量都符合伯努利分布(0-1分布)。强悍的可解释性;
模型训练后可直观的看出特征的推荐权重,从而解释其重要性上极为方便。工程代价小;
模型简单、训练开销小、可并行化。2.1逻辑回归的数学表达
(1)将特征向量化为 x=(1,x1,x2,…,xn)x=(1,x_1,x_2,…,x_n) 形式输入模型。
(2)赋予各特征初试权重 (b,θ1,…,θn)(b,\theta_1,…,\theta_{n}) ,将各特征进行特征求和得到 θTX\theta^TX 。(各特征的差异性可由特征权重体现)
(3)将θTX\theta^TX输入sigmoid函数得到假设函数 hθ(x)h_\theta(x) 。
(4)使用梯度下降、牛顿法等方法训练模型 hθ(x)h_\theta(x) ,得到模型最终的特征权重即预测模型。
sigmoid函数的表达式和函数走势如下图所示:
f(z)=11+e−zf(z)=\frac{1}{1+e^{-z}} \\
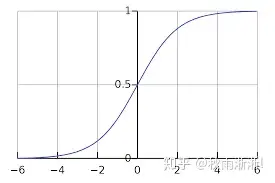
2.2逻辑回归的模型训练方法
以常用的梯度下降为例。
假设函数为 hθ(x)=11+e−θTxh_\theta(x) = \frac{1}{1+e^{-\theta ^T x}} ,那么逻辑回归的模板函数的求解有一下几个步骤。
,对于一个预测样本,其预测为正样本(类别1,点击)和负样本(类别-1,不点击)的概率如下公式所示:
p(y=1|x;θ)=hθ(x)p(y = 1|x;\theta) = h_\theta(x) \\ p(y=−1|x;θ)=1−hθ(x)p(y = -1|x;\theta) =1 – h_\theta(x)\\将上式子综合起来:
p(y|x;θ)=(hθ(x))y(1−hθ(x))1−yp(y|x;\theta) = (h_\theta(x))^y(1-h_\theta(x))^{1-y} \\基于极大似然估计原理,可得出逻辑回归的目标函数如下:
L(θ)=∏i=1mp(y|x;θ)L(\theta) = \prod_{i=1}^{m}p(y|x;\theta) \\ 由于上式的连乘形式不利于梯度求导,一般会在给上式取log。同时一般会给目标函数乘以一个 −(1/m)-(1/m),进而也将原本的求极大值为问题转化为求极小值问题,这样逻辑回归的目标函数的求解会转变为一个凸优化问题,在求解上也带来了便利。
J(θ)=−1m(∑i=1myilog(hθ(xi)+(1−y)ilog(1−hθ(xi))|y=0,1J(\theta) =-\frac{1}{m}(\sum_{i=1}^{m}y^i log(h_\theta(x^{i})+(1-y)^i log(1-h_\theta(x^{i}))|y=0,1\\最后对上式求偏导,对权重参数进行更新后 可得到逻辑回归的训练模型,也即推荐预测模型。
∂∂θjJ(θ)=1m∑i=1m(hθ(xi)−yi)xji\frac{\partial}{\partial\theta_j}J(\theta) = \frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^i) – y^i)x_{j}^{i} \\注:这个求导的推导过程挺长,此处不做展开,不过推导过程也很简单,套用下链式法则就行,墙裂建议读者上手推导,感兴趣的同学可戳笔者这篇文章的中的第三章节:Youtube DNN serving目标解析 | 从odds到Logit 、Logistic Regression逻辑函数的梯度算法看起来很舒适,在计算上也很方便,这或许就是它损失函数如此设计的原因。但是值得注意的是,它的表达上虽然和线性回归一致,但其假设函数 hθ(x)h_\theta(x) 不同,不可一概而论。
2.3逻辑回归的局限性
逻辑回归在推荐领域的应用,解决了部分协同过滤类算法表达能力不足问题,但是站在今年的角度来看,逻辑回归被淘汰的理由如下:
模型表达能力仍旧不够强;无法进行特征交叉、无法直接利用特征之间的组合信息提升推荐准确性,存在信息损失问题。可能会得出错误的推荐结论。由于仅用单一特征进行建模而非多维交叉特征,很容易陷入”辛普森悖论“困境。无法进行良好的特征筛选;不支持在今天看来较为常规的特征选择等”高级“操作。逻辑回归的这些局限带来的性能瓶颈,倒逼这推动着业界人士对更”高阶“算法模型的探索,因而本文回顾的FM推荐模型得以诞世。
3.POLY2模型–FM模型与逻辑规则的”中间者“
FM模型的诞生源于业界人员的这样一种尝试:在逻辑回归的基础上直接增加一个高阶特征组合项目,进而挖掘组合信息。
但一开始,这个高阶项目并不像现在使用的形式,它由单一特征之间两两组合得出,其二阶表达式如下所示:
f(θ,x)=∑i=1n∑j=i+1nθi.jxixjf(\theta,x) = \sum_{i=1}^{n}\sum_{j=i+1}^{n}\theta_{i .j}x_{i}x_{j} \\ 这种特征组合的方式被称为POLY2模型。
POLY2模型的不足之处很容易看出:
模型训练复杂度高、训练开销大;参数量从 nn 上升到 n2n^2 ,模型复杂度与训练压力剧增。模型容易无法收敛;互联网中的数据常常极度稀疏,在进行one by one 的特征组合后,数据的稀疏性会极度上升。在缺乏足够的有效数据时,模型的训练无法收敛。4.因子分解机FM
FM模型通过对二阶组合特征的巧妙设计,较为完美的解决了POLY2模型在增加模型表达能力的基础上带来的新问题,同时在泛化能力等方面有着增强。
FM的模型下式所示:y^=hθ(x)=θ0+∑i=1nθ1xi+∑i=1n−1∑j=i+1n<θi.θj>xixj\hat{y}=h_\theta(x) = \theta_0 +\sum_{i=1}^n{}\theta_1x_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}<\theta_i.\theta_j>x_ix_j \\ 对比FM与POLY2的二阶部分,可以看出两者的主要区别为FM用两个向量的内积 <θi.θj><\theta_i.\theta_j> 代替了单一的权重系数 θi.j\theta_{i .j} 。
这种操作的高明之处在于:
为每个特征学习了一个隐向量权重(latent vector),而这种隐向量的计算方式可以更好地解决数据的稀疏问题,从而提高模型的泛化能力。(隐向量可以认为是embedding,这样会好理解些)隐向量计算特征权重的方式,可将权重参数从POLY2的 n2n^2 级别下降到 nknk 级别(k为隐向量的维度,n>>k)。问题来了:
为什么可以解决稀疏性,提高泛化能力?
假设样本具备两个特征 xix_i 与 xjx_j ,由于数据稀疏xi,xjx_i,x_j 并未同时在训练实例里出现过,即xiandxjx_i \ and \ x_j一起出现的次数为0,按POLY2的计算方式无法学到这特征组合的权重。
但FM为每个特征都学习了一个embedding,这意味着特征xix_i和其它任意特征组合出现过,就可以学习到每个特征对应的embedding向量。即xiandxjx_i and x_j这个特征组合形式没有出现过,但是在预测的时候,如果看到这个新的特征组合,因为xix_i和xjx_j都能学会自己对应的embedding,从而可以通过内积算出这个新特征组合的权重。这是为何说FM模型泛化能力强的根本原因。
为什么可以大幅度降低参数量?
直接上公式
f(x)=∑i=1n∑j=i+1n<vi.vj>xixj=12(∑i=1n∑j=1n<vi.vj>xixj−∑i=1n<vi.vi>xixi)=12(∑i=1n∑j=1n∑f=1k<vi,f.vj,f>xixj−∑i=1n∑f=1k<vi,f.vi,f>xixi)=12∑f=if((∑i=1nvi,f.xi).(∑j=1nvj,f.xj)−∑i=1nvi,f2xi2)=12∑f=1k((∑i=1nvi,f.xi)2−∑i=1nvi,f2xi2)\begin{align*} f(x) &= \sum_{i=1}^{n} \sum_{j=i+1}^{n}<v_i.v_j>x_ix_j \\ & = \frac{1}{2}(\sum_{i=1}^{n}\sum_{j=1}^{n}<v_i.v_j>x_ix_j-\sum_{i=1}^{n}<v_i.v_i>x_ix_i) \\ & = \frac{1}{2}(\sum_{i=1}^{n}\sum_{j=1}^{n}\sum_{f=1}^{k} <v_{i,f}.v_{j,f}> x_ix_j – \sum_{i=1}^{n}\sum_{f=1}^{k}<v_{i,f}.v_{i,f}>x_ix_i)\\ & = \frac{1}{2}\sum_{f=i}^{f}((\sum_{i=1}^{n}v_{i,f}.x_i).(\sum_{j=1}^{n}v_{j,f}.x_j) – \sum_{i=1}^{n}v_{i,f}^{2}x_{i}^{2})\\ & = \frac{1}{2}\sum_{f=1}^{k}((\sum_{i=1}^{n}v_{i,f}.x_i)^2 – \sum_{i=1}^{n}v_{i,f}^{2}x_i^2) \end{align*} \\
从上述公式可以看到,虽然FM的二阶部分的原始表达方式为 kn2kn^2 级别的参数量级,但是经过一系列的恒等变化,可以将FM的二阶参数成功的降为了 knkn 级,同时在数值计算上也仍旧优雅。
4.1 FM的模型训练
FM模型的低阶逻辑回归的训练在前文已经有很详细的推导过程,这里主要推导一下二阶部分的训练。
首选需要定义一个损失函数
从sigmoid函数 σ\sigma 谈起,其有一个优良的特性: 1−σ(x)=σ(−x)1-\sigma(x)=\sigma(-x) \\ 推理如下:σ(x)=11+e−x=ex1+ex\sigma(x) = \frac{1}{1+e^{-x}} = \frac{e^x}{1+e^x} \\
σ(x)+σ(−x)=ex1+ex+11+ex=1\sigma(x) +\sigma(-x) = \frac{e^x}{1+e^x}+\frac{1}{1+e^x}=1 \\ 那么若样本标签值用+1与-1表示正负值时,存在:
当y=1时, p(y=1|x;θ)=σ(y^)p(y = 1|x;\theta) =\sigma(\hat{y}) 当y=-1时,p(y=−1|x;θ)=1−σ(−y^)=σ(y^)p(y = -1|x;\theta) =1-\sigma(-\hat{y}) = \sigma(\hat{y})那么对于预测数据存在:
p(y|x)=σ(yy^)p(y|x)=\sigma(y\hat{y})\\
采用Logistic loss则可得到FM的损失函数如下:
L=−logσ(yy^)=−log11+e−yy^L=-log\sigma(y\hat{y})=-log\frac{1}{1+e^{-y\hat{y}}} \\
其损失函数 LL 的求导如下所示: ∂L∂θ=−logσ(yy^)∂θ=−1σ(yy^).∂σ(yy^)∂θ=−1σ(yy^).σ(yy^)(1−σ(yy^)).y∂y^∂θ=(σ(yy^)−1).y.∂y^∂θ\begin{align*} \frac{\partial L}{\partial \theta}&= -\frac{log \sigma(y\hat{y})}{\partial \theta} \\ &=-\frac{1}{\sigma(y\hat{y})}.\frac{\partial \sigma(y\hat{y}) }{\partial \theta} \\ &=-\frac{1}{\sigma(y\hat{y})}.\sigma(y\hat{y})(1-\sigma(y\hat{y})).y\frac{\partial \hat{y} }{\partial \theta}\\ &=(\sigma(y\hat{y})-1).y.\frac{\partial \hat{y}}{\partial \theta} \end{align*} \\
FM的假设函数 y^\hat{y} 的表达式如下:
y^=θ0+∑i=1nθ1xi+∑i=1n−1∑j=i+1n<θi.θj>xixj=θ0+∑i=1nθ1xi+12∑f=1k((∑i=1nθi,f)2−∑i=1nθi,f2xi2)\begin{align*} \hat{y} &= \theta_0 +\sum_{i=1}^{n}\theta_1x_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}<\theta_i.\theta_j>x_ix_j \nonumber \\ &= \theta_0 +\sum_{i=1}^{n}\theta_1x_i+ \frac{1}{2}\sum_{f=1}^{k}((\sum_{i=1}^{n}\theta_{i,f})^2 – \sum_{i=1}^{n}\theta_{i,f}^{2}x_i^2) \nonumber \end{align*} \\
y^\hat{y} 的一阶导数较容易求出,二阶部分的求导如下:
left=∂12∑f=1k(∑i=1nθi,fxi)2∂θi,f=∑f=1k(∑i=1nθi,fxi).∂∑i=1nθi,fxi∂θi,f=(∑i=1nθi,fxi).xi\begin{align*} left&=\frac{\partial \frac{1}{2}\sum_{f=1}^{k}( \sum_{i=1}^{n} \theta_{i,f} x_i)^2}{\partial \theta_{i,f}} \nonumber \\ &=\sum_{f=1}^{k} (\sum_{i=1}^{n}\theta_{i,f}x_i ).\frac{\partial \sum_{i=1}^{n} \theta_{i,f}x_i}{\partial \theta_{i,f}}\nonumber \\ &=(\sum_{i=1}^{n}\theta_{i,f}x_i).x_i \\ \end{align*} \\
)right=−∂12∑f=1k(∑i=1nθi,f2xi2)∂θi,f=−12xi2.2θi,f=−xi2θi,f\begin{align*} right&=-\frac{\partial \frac{1}{2}\sum_{f=1}^{k}(\sum_{i=1}^{n}\theta_{i,f}^2x_i^2)}{\partial \theta_{i,f}} \nonumber\\ &=-\frac{1}{2}x_i^2 .2\theta_{i,f}\nonumber \\ &=-x_i^2\theta_{i,f}\\ \end{align*} \\ 结合低阶项目导数,最终得到FM的损失函数导数为:
∂y^∂θ={1xi(∑i=1nθi,fxi).xi−xi2θi,f\frac{\partial \hat{y}}{\partial \theta} = \begin{cases} 1 \\ x_i \\ (\sum_{i=1}^{n}\theta_{i,f}x_i).x_i-x_i^2\theta_{i,f} \end{cases} \\
所以FM模型中参数求解过程如下:
{ω0=ω0−α(σ(yy^)−1)yω=ω0ω1=ω1−α(σ(yy^)−1)yxiω=ω1v=v−α(σ(yy^)−1)y(∑i=1nθi,fxi).xi−xi2θi,fω=v\left \{ \begin{array}{ll} \omega_0 = \omega_0-\alpha(\sigma(y\hat{y})-1)y & {\omega = \omega_0}\\ \omega_1 = \omega_1-\alpha(\sigma(y\hat{y})-1)yx_i & {\omega = \omega_1}\\ v = v-\alpha(\sigma(y\hat{y})-1)y(\sum_{i=1}^{n}\theta_{i,f}x_i).x_i-x_i^2\theta_{i,f} & {\omega = v} \end{array} \right.\\
其中 ,参数项由 ω0\omega_0 表示,一阶项参数由 ω1\omega_1 表示,二介参数由 vv 表示。
至此,FM的模型训练推导结束。
4.2 FM的代码编写与实际应用
FM在二分类问题上的应用
代码如下:














暂无评论内容