如何解释「卷积神经网络」？-卡咪卡咪哈-一个博客

阅读提醒，本文以严谨为主，兼顾理解。

目标

介绍CNNs的基础结构和训练方法。

理解本文所需知识: 高中数学，高中语文

完全读懂本文所需知识: 微积分，线性代数

为了大众阅读，在英文第一次出现的时候，会有标注汉语。

概述

神经网络(neual networks)是人工智能研究领域的一部分，当前最流行的神经网络是深度卷积神经网络(deep convolutional neural networks, CNNs)，虽然卷积网络也存在浅层结构，但是因为准确度和表现力等原因很少使用。目前提到CNNs和卷积神经网络，学术界和工业界不再进行特意区分，一般都指深层结构的卷积神经网络，层数从”几层“到”几十上百“不定。

CNNs目前在很多很多研究领域取得了巨大的成功，例如: 语音识别，图像识别，图像分割，自然语言处理等。虽然这些领域中解决的问题并不相同，但是这些应用方法都可以被归纳为:

CNNs可以自动从(通常是大规模)数据中学习特征，并把结果向同类型未知数据泛化。

背景

半个世纪以前，图像识别就已经是一个火热的研究课题。

1950年中-1960年初，感知机吸引了机器学习学者的广泛关注。这是因为当时数学证明表明，如果输入数据线性可分，感知机可以在有限迭代次数内收敛[1]。感知机的解是超平面参数集，这个超平面可以用作数据分类。然而，感知机却在实际应用中遇到了很大困难，因为1)多层感知机暂时没有有效训练方法，导致层数无法加深，2)由于采用线性激活函数，导致无法处理线性不可分问题，比如“与或”。

这些问题随着后向传播(back propagation，BP)算法和非线性激活函数的提出得到解决。1989年，BP算法被首次用于CNN中处理2-D信号(图像)。

2012年，ImageNet挑战赛中CNN证明了它的实力，从此在图像识别和其他应用中被广泛采纳。

通过机器进行模式识别，通常可以被认为有四个阶段:

数据获取: 比如数字化图像预处理: 比如图像去噪和图像几何修正特征提取：寻找一些计算机识别的属性，这些属性用以描述当前图像与其它图像的不同之处数据分类：把输入图像划分给某一特定类别

CNN是目前图像领域特征提取最好的方式，也因此大幅度提升了数据分类精度，我将在下文详细解释。

网络结构

基础的CNN由卷积(convolution), 激活(activation), and 池化(pooling)三种结构组成。CNN输出的结果是每幅图像的特定特征空间。当处理图像分类任务时，我们会把CNN输出的特征空间作为全连接层或全连接神经网络(fully connected neural network, FCN)的输入，用全连接层来完成从输入图像到标签集的映射，即分类。当然，整个过程最重要的工作就是如何通过训练数据迭代调整网络权重，也就是后向传播算法。目前主流的卷积神经网络(CNNs)，比如VGG, ResNet都是由简单的CNN调整，组合而来。

这些加粗名词将会在下文详细解释。

CNN

图1 某个stage内CNN工作原理

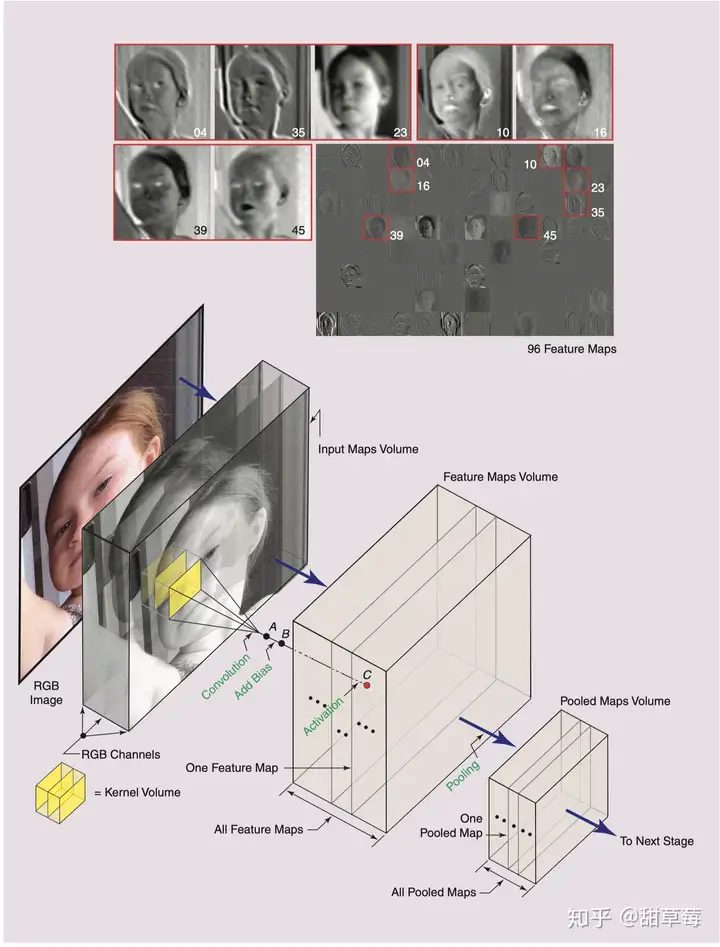
图1显示的是CNN的基础结构，现在大型深层的卷积神经网络(CNNs, 请注意这里是复数)通常由多个上述结构前后连接、层内调整组成，根据功能不同，我们称这些前后连接的结构处于不同阶段(stage)。虽然在主流CNNs中，不同stage里CNN会有不同的单元和结构，比如卷积核 (kernel)大小可能不同，激活函数(activition function) 可能不同，pooling操作可能不存在，但是图1的CNN结构应当能够包含所有的情况。

我们跟随图1来解释，一个stage中的一个CNN，通常会由三种映射空间组成(Maps Volume, 这里不确定是不是应该翻译为映射空间，或许映射体积会更准确),

输入映射空间(input maps volume）特征映射空间(feature maps volume）池化映射空间(pooled maps volume)

例如图中，输入的是彩色RGB图像，那么输入的maps volume由红，黄，蓝三通道/三种map构成。我们之所以用input map volume这个词来形容，是因为对于多通道图像输入图像实际上是由高度，宽度，深度三种信息构成,可以被形象理解为一种”体积”。这里的“深度”，在RGB中就是3，红，黄，蓝三种颜色构成的图像，在灰度图像中，就是1。

卷积

CNN中最基础的操作是卷积convolution，再精确一点，基础CNN所用的卷积是一种2-D卷积。也就是说，kernel只能在x,y上滑动位移，不能进行深度 (跨通道) 位移。这可以根据图1来理解，对于图中的RGB图像，采用了三个独立的2-D kernel，如黄色部分所示，所以这个kernel的维度是 $X\timesY\times3$ X\times Y \times 3 。在基础CNN的不同stage中，kernel的深度都应当一致，等于输入图像的通道数。

卷积需要输入两个参数，实质是二维空间滤波，滤波的性质与kernel选择有关，CNN的卷积是在一个2-D kernel 和输入的 2-D input map 之间，RGB中各图像通道分别完成。

我们假设单一通道输入图像的空间坐标为 $(x,y)$ (x,y) ，卷积核大小是 $p\timesq$ p \times q ，kernel权重为 $w$ w ,图像亮度值是 $v$ v ，卷积过程就是kernel 所有权重与其在输入图像上对应元素亮度之和，可以表示为,

$convx,y=\sumip*qwivi$ conv_{x,y} = \sum_i^{p*q}w_iv_i 。

我们可以用一个例子来说明,

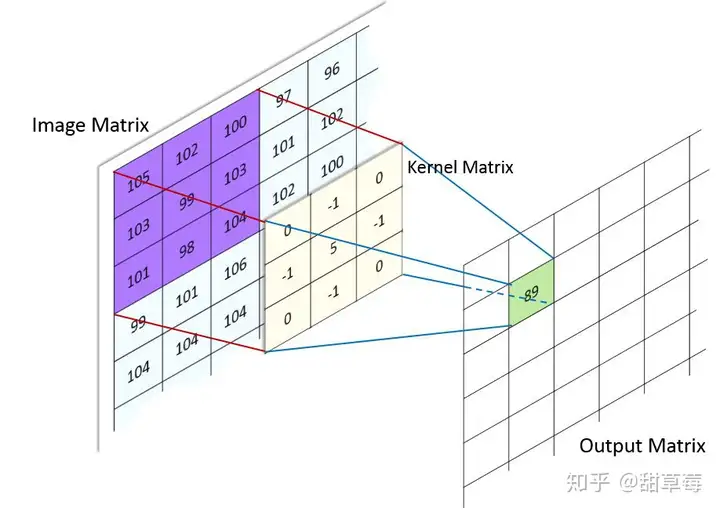
如上图所示，这时候输出的单一元素是

$convx,y=105*0+102*(-1)+100*0+103*(-1)+99*5+103*(-1)+101*0+98*(-1)+104*0=89$ conv_{x,y} = 105*0 + 102*(-1)+100*0+103*(-1)+99*5 +103*(-1)+101*0+98*(-1)+104*0\\ =89

并将kernel随(x,y)平移扫描，可以得到输出空间，这时假设输入图像大小是 $512\times512$ 512 \times 512 ，卷积核是 $3\times3$ 3 \times 3 ，在不考虑零填充（zero padding）的情况，输出是 $(512-3+1)=510\times510.$ (512-3+1)=510 \times 510.

注意卷积层的kernel可能不止一个，扫描步长，方向也有不同，这些进阶方式可以归纳一下:

可以采用多个卷积核，设为n 同时扫描，得到的feature map会增加n个维度，通常认为是多抓取n个特征。可以采取不同扫描步长，比如上例子中采用步长为n, 输出是

（） （510/n,510/n）

（510/n,510/n）padding，上例里，卷积过后图像维度是缩减的，可以在图像周围填充0来保证feature map与原始图像大小不变深度升降，例如采用增加一个1*1 kernel来增加深度，相当于复制一层当前通道作为feature map跨层传递feature map,不再局限于输入即输出, 例如ResNet跨层传递特征，Faster RCNN 的POI pooling

激活

卷积之后，通常会加入偏置(bias), 并引入非线性激活函数(activation function)，这里定义bias为b，activation function 是 $h()$ h() ，经过激活函数后，得到的结果是,

$zx,y=h(\sumip*qwivi+b)$ z_{x,y}=h(\sum_i^{p*q}w_i v_i+b) .

这里请注意，bias不与元素位置相关，只与层有关。主流的activation function 有,

线性整流单元(ReLU):

h(z)=max(0,z)

h(z) = max (0,z)

Sigmoid函数：

h(z)=1/(1+e-z)

h(z)=1/(1+e^{-z})

tanh函数:

h(z)=tanh(z)

h(z)=tanh(z)

根据实际参数大小等性质调整。

图1中feature maps volume的每个元素就是由 $zx,y$ z_{x,y} 。我们可以回到图1的上半部分，这里的feature map是可以可视化的。为了保证阅读体验，我这里再把图1粘贴一遍，

例如采用277*277的RGB图像，采用96个11*11*3的kernels同时扫描，很容易得到输出的feature maps是96个267*267的二维 feature map, 267*267是单个图像feature map的x,y轴大小，96是卷积核个数，原本的3通道在积分的时候会被作为一个元素加起来。如上图，这些feature map可视化之后，可以看到4 和35表示边缘特征，23是模糊化的输入，10和16在强调灰度变化，39强调眼睛，45强调红色通道的表现。

池化

池化(pooling），是一种降采样操作(subsampling)，主要目标是降低feature maps的特征空间，或者可以认为是降低feature maps的分辨率。因为feature map参数太多，而图像细节不利于高层特征的抽取。

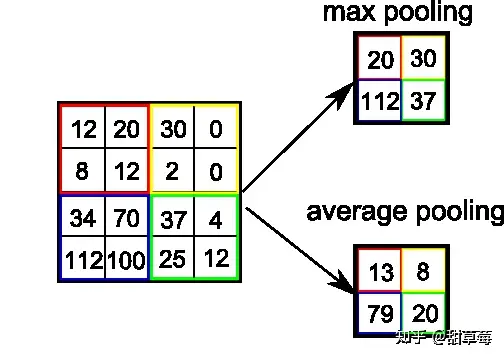
目前主要的pooling操作有:

最大值池化 Max pooling：如上图所示，2 * 2的max pooling就是取4个像素点中最大值保留平均值池化 Average pooling: 如上图所示, 2 * 2的average pooling就是取4个像素点中平均值值保留L2池化 L2 pooling: 即取均方值保留

Pooling操作会降低参数，降低feature maps的分辨率，但是这种暴力降低在计算力足够的情况下是不是必须的，并不确定。目前一些大的CNNs网络只是偶尔使用pooling.

以上是一个CNN stage的基本结构，需要强调的是，这个结构是可变的，目前大部分网络都是根据基本结构堆叠调整参数，或跳层连接而成。CNN的输出是feature maps，它不仅仅可以被输入全连接网络来分类，也可以接入另外一个“镜像”的CNN，如果输入图像维度与这个新的CNN输出feature maps特征维度相同，即这个新接入的CNN在做上采样, upsampling，得到的图像可以认为是在做像素级的标注，图像分割[2]。

全连接网络

出现在CNN中的全连接网络(fully connected network)主要目的是为了分类, 这里称它为network的原因是，目前CNNs多数会采用多层全连接层，这样的结构可以被认为是网络。如果只有一层，下边的叙述同样适用。它的结构可能如下图所示:

图2，全连接层结构

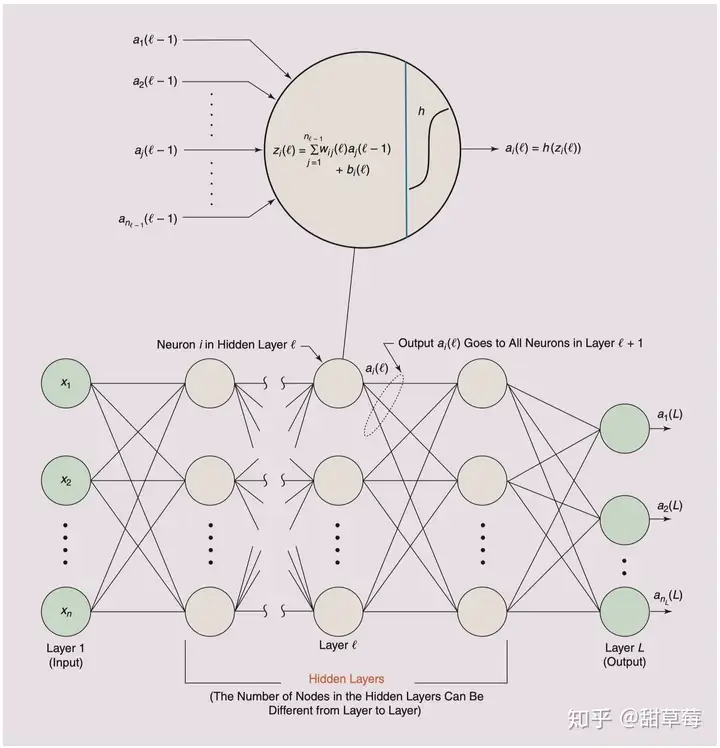
不同于CNN的滑动卷积，全连接网络每一层的所有单元与上一层完全连接。通常，除了输入层和输出层的其他层，都被认为是隐含层。如图2所示，对于第 $l$ l 层的第 $i$ i 个神经元，它的输出计算方式是,

$zi(l)=\sumj=inl-1wij(l)aj(l-1)+bi(l),$ z_i(l)=\sum_{j=i}^{n_{l-1}}w_{ij}(l)a_j(l-1)+b_i(l),

考虑activation function之后，对于第 $l$ l 层的第 $i$ i 个神经元，输出是

$ai(l)=h(zi(l)).$ a_i{(l)}=h(z_i(l)).

计算这一层中的所有神经元之后, 作为下一层的输入。

全连接网络和CNN的数学表达结构其实很相似，只是不存在关于图像空间上的滑动卷积。

目标函数与训练方法（数学高能预警）

CNN网络的训练误差需要通过一个目标函数来衡量，目前比较流行的目标函数是均方误差(Mean Square Error)和K-L散度（K-L divergence)，对于输出层的误差公式很容易判断:

MSE:

E=12\sumj=1nL(rj-aj(L))2,

E = \frac{1}{2}\sum_{j=1}^{n_L}(r_j-a_j(L))^2, —————————-（1）K-L divergence :

E=-1nL\sumj=1nL[rjlnaj(L)+(1-rj)ln(1-aj(L))]

E = – \frac{1}{n_L}\sum_{j=1}^{n_L}[r_j\ln a_j(L)+(1-r_j)\ln(1-a_j(L))]

其中 $rj$ r_j 是期望输出(标注标签), $aj(L)$ a_j(L) 是第 $L$ L 层的第 $j$ j 个神经元的输出。

K-L divergence 和MSE原理本文不再过多介绍，通常K-L divergence的权重更新会比MSE更快，不过本文将通过MSE来举例说明，

如果我们仅仅考虑最后一层的更新，通过梯度下降，权重 $wij$ w_{ij} 和 $bi$ b_i 的更新方式把 $aj(L)$ a_j(L) 代入公式求导就可以算出,

$wij(l):=wij(l)-α\nablaE\nablawij(l)$ w_{ij}(l):=w_{ij}(l)-\alpha\frac{\nabla E}{\nabla w_{ij}(l)} 和 $bi(l):=bi(l)-α\nablaE\nablabi(l)$ b_{i}(l):=b_{i}(l)-\alpha\frac{\nabla E}{\nabla b_{i}(l)} —(6)

其中 $α$ \alpha 是learning rate, 如果learning rate 取值过大，可能会收敛于震荡，如果learning rate取值过小，可能收敛速度太慢。

以上是如果网络只有最后一层的训练方式，但是实际上对于深层网络，我们很难一次通过数学计算出每一层的权重更新公式，也就是权重很难更新。

可以看出，如果想要训练网络，就需要根据误差更新权重，而如果想要获得误差 $E$ E ，不论是MSE,还是K-L divergence, 都需要两种参数：期望输出 $r$ r ,和当前层权重 $a$ a (回顾公式，即 $w,b$ w,b )。其中期望输出 $r$ r 来自标签集，很容易获得，而 $a$ a 和误差 $E$ E 相互影响。那么，解决方式就很明显，我们可以先固定一方，更新另一方，这是alternating optimazition优化多参数模型的经典思路。CNN的训练方法思路也来自于此，被称作backpropagation。

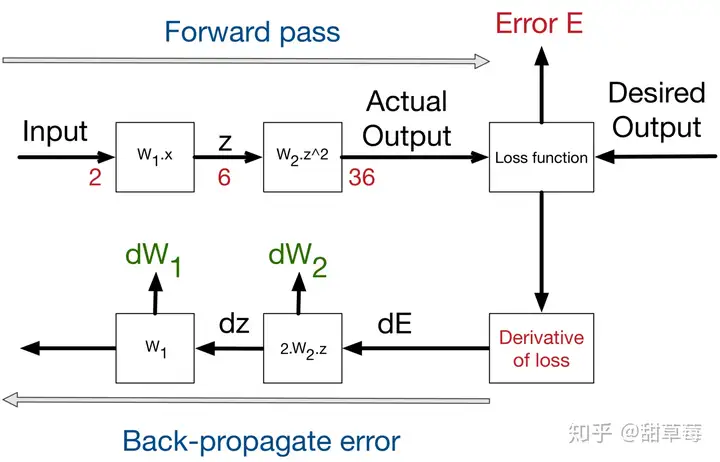
Backpropagation算法，大概可以分为两步:

1. 通过训练数据计算网络中的所有 $a$ a ，这里可以回想一下 $a$ a 的计算方法，最初的 $a$ a 只需要输入图像和初始化权重就可以计算，这一步是从输入图像到输出层的计算，即上图中的前向传播。

2. 获得所有 $a$ a 之后，再我们就可以通过目标函数和期望输出计算出最后一层的 $E$ E ,而有了最后一层的 $E$ E ，可以计算出倒数第二层的期望输出 $r$ r ，以此类推，可以计算误差到第一层，并通过求导更新权重。这是上图的后向误差传播（这里表述不严谨)。

上述1，2部操作会交替进行。

实际上BP算法通过以下四个公式更新:

$\nablaE\nablawij(l)=aj(l-1)Δi(l)$ \frac{\nabla{E}}{\nabla{w}_{ij}(l)} = {a}_{j}(l-{1}){\Delta}_{i}(l) ———(2)

$\nablaE\nablabi(l)=Δi(l)$ \frac{\nabla{E}}{\nabla{b}_{i}(l)} = {\Delta}_{i}(l) ———–(3)

$Δj(l)=h'(zj(l))\sumiwij(ℓ+1)Δi(l+1)$ \Delta_j(l) = {h}\left({z}_{j}(l)\right)\mathop{\sum}\limits_{i}{w}_{ij}(\ell + {1}){\Delta}_{i}(l+ {1}) ——–（4）

$Δj(L)=h'(zj(L))[aj(L)-rj]$ \Delta_j({L}) = {h}({z}_{j}(L))[{a}_{j}({L})-{r}_{j}] ———–（5）

(2)和(3)用来计算更新权重 $wi,j$ w_{i,j} 和bias $bi$ b_i 的所需的梯度(请往上回顾一下单层权重更新部分)

(4)和(5)是(2)和(3)中未知项的来源，(5)用来计算最后一层梯度，(4)用来计算除最后一层外其他层的梯度,并通过传播梯度来传递误差，其中activition function的梯度 $h'(zj(l)),l=1,\dots,L$ {h}({z}_{j}(l)),l=1,…,L 和各层权重 $ai(l),l=1,\dots,L$ a_i(l), l=1,…,L 都可以在前向传播过程中计算出来。

严谨的BP算法流程:

1. 用随机小数初始化所有权重 $wi,j$ w_{i,j} 和bias $bi$ b_i ;

2. 利用来自训练集的输入向量(例如一副图像)，算出所有的 $aj(l)$ a_j(l) 和 $h'(zj(l))$ {h}({z}_{j}(l))

3.用公式(1)计算 MSE或K-L divergence

4. 用(5）计算 \Delta_j({L}) , 并后向传播，用(4)计算出所有其他层的 \Delta_j(l) , l=L-1,L-2,….,2

5. 利用（6）更新权重

6. 对训练集中的所有输入向量(图像)重复 2-5，完成一次所有训练成为一个epoch。当MSE误差稳定不变，或者到达某个迭代次数后，BP算法停止。

这就是CNNs的训练过程。

完。

[1] F. Rosenblatt, “Two theorems of statistical separability in the perceptron,” in Proc. Symp. No. 10 Mechanisation Thought Processes, London, 1959, vol. 1, pp. 421–456.

[2] E. Shelhamer, J. Long, and T. Darrell, “Fully convolutional networks for semantic segmentation,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 39, no. 4, pp. 640–651, 2017.

[3] Gonzalez R C. Deep Convolutional Neural Networks [Lecture Notes][J]. IEEE Signal Processing Magazine, 2018, 35(6): 79-87.

[4] Y. LeCun, Y. Bengio, and G. E. Hinton, “Deep learning,” Nature, vol. 521, pp. 436–444, May, 2015.

[5] Y. LeCun, B. Boser, J. S. Denker D. Henderson,R. E. Howard, W. Hubbard, and L. D. Jackel, “Backpropagation applied to handwritten zip code recognition,” Neural Comput., vol. 1, no. 4, pp. 541–551, 1989.

THE END