全面了解卷积神经网络

背景四类解决方案解决图片的不变性（from PRML）简介理解卷积卷积层汇聚层归一化层整体架构小结

背景

20世纪60年代，Hubel和Wiesel在研究猫脑皮层中用于局部敏感和方向选择的神经元时发现其独特的网络结构可以有效地降低反馈神经网络的复杂性，继而提出了卷积神经网络（Convolutional Neural Networks-简称CNN）

同时，人眼在识别图像时，往往从局部到全局，局部与局部之间联系往往不太紧密。结合到神经网络，我们发现我们不需要神经网络中的每个结点都掌握全局的知识，因此可以从这里可以大量减少需要学习的参数数量

需要注意的是CNN的思想和BP网络是相反的，BP网络认为，大脑每个神经元都要感知物体的全部（全像素全连接）,并且只是简单的映射，并没有对物体进行抽象处理。而卷积神经网络（Convolution Neural Network）最先证明了BP网络的不科学性，然后在各种任务中大放异彩！

四类解决方案解决图片的不变性（from PRML）

我们知道，在很多图片中，比如都存在一只猫，那只猫的姿态或者形态是非常不同的，在我们人类看来这没什么，很容易知道它都是一只猫，但是，在计算机看来，就没有那么简单了，关于这种图片内容的不变性，我们可以有如下的方法来解决：Data Augmentation：用多种变化后生成不同样本的图片Tangent Propagation：用正则项的方式，用一个函数Invariant feature：用一些特征来做不变性Neural Network structure with invariant properties (e.g. CNN)：用一些特征结构，比如CNN中的卷积

简介

卷积神经网络主要由三种类型的层构成：卷积层，汇聚（Pooling）层和全连接层（全连接层和常规神经网络中的一样）。通过将这些层叠加起来，就可以构建一个完整的卷积神经网络。有的层有参数，有的没有（卷积层和全连接层有，非线性（ReLU）层和汇聚层没有）。有的层有额外的超参数，有的没有（卷积层、全连接层和汇聚层有，非线性（ReLU）层没有）。

然后下面是一个简单的cnn神经网络结构的例子：

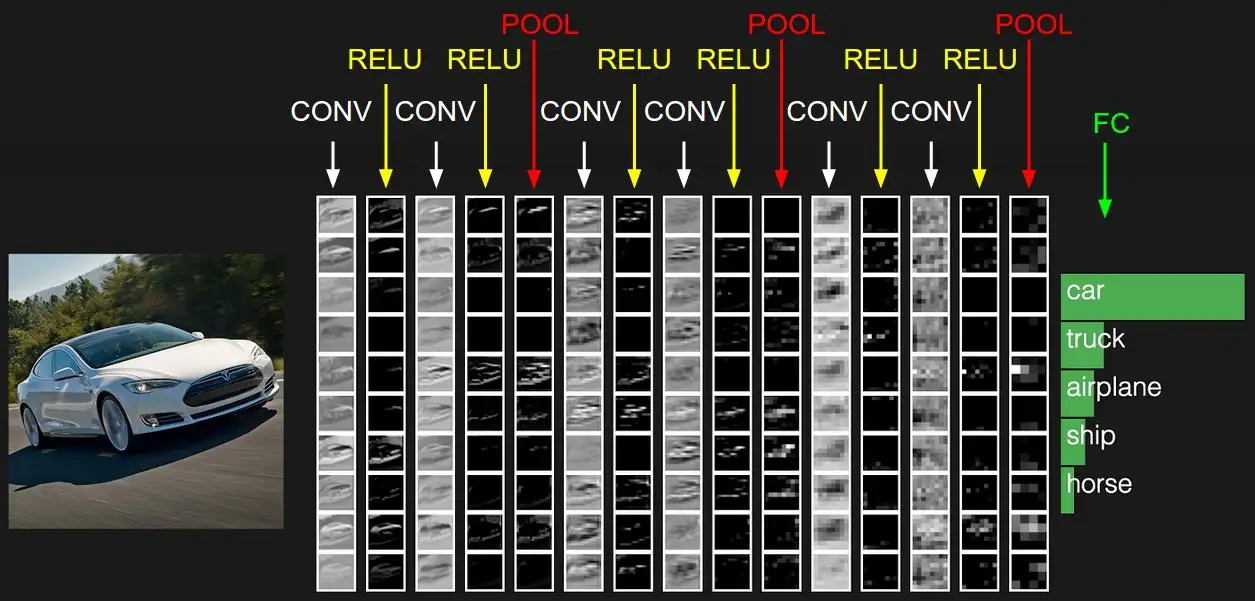
理解卷积

首先来看通俗理解，比如往一片平静的水面投入一块石头，水面的波纹随时间推移扩散开去，在水面还没有变为平静前，再投入一颗石头，也产生波纹，这时候当两个波纹相混合时，就会发现波纹成了另一种，而且不是两种波纹的直接叠加。这就是一种卷积，所以简单来说，卷积就是两个函数（上面例子的两种波纹）互相作用产生的一个新函数（上面例子就是新的波纹）

再来一个更加接近定义的例子：假如你被别人打了一拳，这一拳会在1小时疼痛消失[这一拳轻重不同，所以虽说都在一个小时消失，但是在1个小时内感觉的疼痛也不一样。设最轻(注意)的一拳在一小时内的疼痛感觉函数为h(t），二倍的最轻力度打你，疼痛感就是2h(t)对吧，f(n)倍最轻力度，就是f(n)h(t)了吧]，当别人在一小时内在第一秒，第二秒，第三秒…..第六十秒……动武时，可设f(n)为每次的轻重函数，这就是说在0到2小时内你会感觉疼，那么在这0到2小时的任意一个时刻的疼痛程度Y(t)怎么表示呢？（自己先可以算一下，算出来的话下面的就不用看啦）——肯定是每拳的疼痛效果叠加啦，既0到n的f(n)h(t-n)相加，如f(1)h（t－1）＋f(2)h(t-2)……，当n很小时，为0.00000001时，就可以用积分符号来代替求和。n次抽象为τ就是我们平时的f(t)与h(t)的卷积啦！

第二个例子摘自如何通俗易懂地解释卷积–冯小帅的回答

然后简述下定义，简单定义：卷积是分析数学中一种重要的运算。设:f(x),g(x)是R上的两个可积函数，作积分：

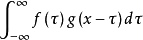
可以证明，关于几乎所有的实数x，上述积分是存在的。这样，随着x的不同取值，这个积分就定义了一个新函数h(x)，称为函数f与g的卷积，记为h(x)=(f*g)(x)。

或者说，卷积是两个变量在某范围内相乘后求和的结果。如果卷积的变量是序列x(n)和h(n)，则卷积的结果

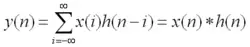
其中星号*表示卷积。当时序n=0时，序列h(-i)是h(i)的时序i取反的结果；时序取反使得h(i)以纵轴为中心翻转180度，所以这种相乘后求和的计算法称为卷积和，简称卷积。另外，n是使h(-i)位移的量，不同的n对应不同的卷积结果。（注意这里就是符合神经网络卷积计算的）

如果卷积的变量是函数x(t)和h(t)，则卷积的计算变为

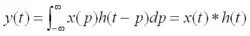
其中p是积分变量，积分也是求和，t是使函数h(-p)位移的量，星号*表示卷积

最后说应用，在其他很多领域卷积都有广泛的应用，比如统计学，物理学，声学等等。这里主要说说在神经网络中的应用：假如用一个模板和一幅图像进行卷积，对于图像上的一个点，让模板的原点和该点重合，然后模板上的点和图像上对应的点相乘，然后各点的积相加，就得到了该点的卷积值。对图像上的每个点都这样处理，而在神经网络中，就直接可以看作加权求和 由于大多数模板都是对称的，所以模板不旋转也可以。

也就是说，运算和之前全连接的神经网络是一模一样的，CNN只是在局部上加权求和，其中以上说的模板就是下面的卷积核。

然后下面以层到层的顺序来详细讲解cnn，其中全连接在之前神经网络的文章也做讲解，详细看之前文章！

卷积层

注意，以下讨论的前提是你熟悉了传统ANN的网络结构和一般知识，不明白的可以先看下我专栏前面的文章。

卷积计算

卷积层的参数是有一些可学习的卷积核集合构成的。每个卷积核在空间上（宽度和高度）都比较小，但是深度和输入数据一致。在每个卷积层上，我们会有一整个集合的卷积核（比如12个），每个都会生成一个不同的二维激活图，一个激活图对应的得到图像的一种特征，也就是原来三维的图像变成一个二维的特征激活图。将这些激活映射在深度方向上层叠起来就生成了输出数据。

注意：多个卷积核就是对应在提取不同的方面的特征，比如颜色，轮廓，背景等等。

普通深度神经网络就是隐含层的数量较多，导致参数增多，而我们可以认为卷积层比起常见的全连接层的重要特点就是减少参数的数量。在深度一致的时候，n*n的卷积核对m*m的图片做卷积运算的话，就会产生（m-n）/1+1（注意那个除以1是步长，在这里步长是1，当然也可以设置成其他的值，除不尽的情况是在外围加上几层，使得可以整除）的新的生成层，所以最重要的就是能整除.

注意：我们倾向于选择多层小size的卷积层，而不是一个大size的卷积层。比如3×3,5×5。

然后进一步解释几个超参数，一个是输出数据体的深度，它和使用的卷积核的数量一致，而每个卷积核在输入数据中寻找一些不同的东西，也就是对应不同的特征（这里注意和上面卷积核的深度是不一样的概念！）。另一个是卷积核在滑动的时候的步长。当步长为1，卷积核每次移动1个像素。当步长为2（或者不常用的3，或者更多，这些在实际中很少使用），卷积核滑动时每次移动2个像素。这个操作会让输出数据体在空间上变小。还有一个就是零填充尺寸，将输入数据体用0在边缘处进行填充，使得卷积核在滑动是可以正好滑满整个输入数据体，当然，其作用就是控制输出数据体的空间尺寸。

举个例子： 假设输入数据体尺寸为[32x32x3]（比如CIFAR-10的RGB图像），如果卷积核是5×5的宽度×广度，那么卷积层中的每个神经元会有输入数据体中[5x5x3]区域的权重，共5x5x3=75个权重（还要加一个偏差参数）。注意这个连接在深度维度上的大小必须为3，和输入数据体的深度一致。

如图，一个二维的图像（没有三通道，只有一通道）做卷积的图示：

当然，也可以看下CS231n卷积计算例子，其中有个三维图（三通道）动态卷积运算。挺直观的！

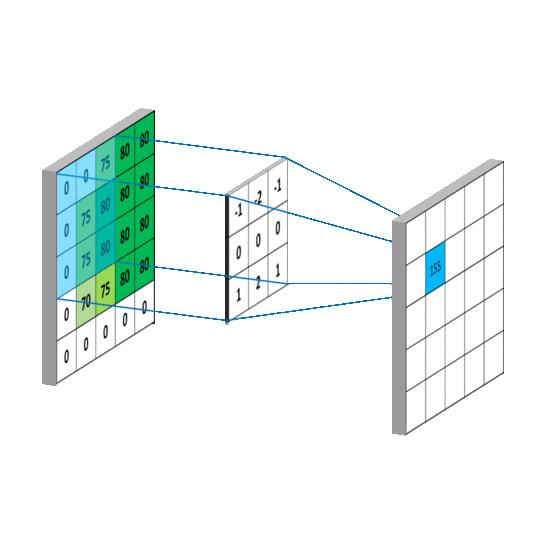
局部连接

受启发于生物学里面的视觉系统结构，也就是动物视觉皮层的神经元就是局部接受信息的（即这些神经元只响应某些特定区域的刺激），CNN采样了局部连接（及其重要的特征），这样做的效果很好，且减少大量参数！

左图为全连接，右图为局部连接

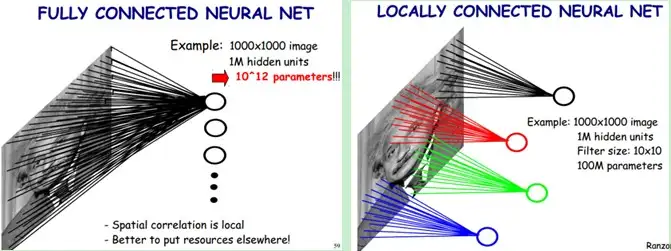
左图中，参数是10的12次方个。右图中，当隐层的数量一样（1m个）时，且卷积核是10×10，那么权值数据为1000000×100个参数，减少为原来的万分之一。所以卷积运算能大大的减少了参数的数量。

参数共享

CNN还有一个降低参数数目的重要特性，就是参数共享。而可以参数共享的原因是如果在图像某些地方探测到一个水平的边界是很重要的，那么在其他一些地方也会同样是有用的，这是因为图像结构具有平移不变性。所以在卷积层的输出数据体的5×5个不同位置中，就没有必要重新学习去探测一个水平边界了。也就是说如果说一个卷积核在图片的一小块儿区域可以得到很好的特征，那么在其他的地方，也可以得到很好的特征。结合到具体，就是一个卷积核对图像做一次卷积得到一个二维特征激活图，若这个激活图一共n个元素，然后激活图中每个元素通常是被非线性（ReLU）层激活，这样的话就类似于一个激活图相当于n神经元，但这些神经元共享一个卷积核，也就是参数是一样的！

下面就是一组固定的权重和不同窗口内数据做卷积，且不同的卷积核（或叫filter）得到不同的特征激活图：

相对全连接传统神经网络，CNN的参数较少的原理就是参数共享和局部连接。

1×1的卷积大概有两个方面的作用：

实现跨通道的交互和信息整合(NIN)进行卷积核通道数的降维和升维(Residual network,google net)下一篇文章也会结合论文讲述!

汇聚层

在连续的卷积层之间会周期性地插入一个汇聚层。它的作用是逐渐降低数据体的空间尺寸，这样的话就能减少网络中参数的数量，使得计算资源耗费变少，也能有效控制过拟合，提取重要特征，符合不变性。最常见的形式是汇聚层使用尺寸2×2的滤波器，以步长为2来对每个深度切片进行降采样，将其中75%的激活信息都丢掉。每个MAX操作是从4个数字中取最大值（也就是在深度切片中某个2×2的区域）。深度保持不变。

在池化单元内部能够具有平移的不变性，它的平移范围也是有一定范围的，因为每个池化单元都是连续的，所以能够保证图像整体上发生了平移一样能提取特征进行匹配。一般来说，都是用max或者是mean（或Average），而max还是mean都是在提取区域特征，均相当于一种抽象，抽象就是过滤掉了不必要的信息（当然也会损失信息细节），所以在抽象层次上可以进行更好的识别。至于max与mean效果是否一样，还是要看需要识别的图像细节特征情况，这个不一定的，不过据说差异不会超过2%。

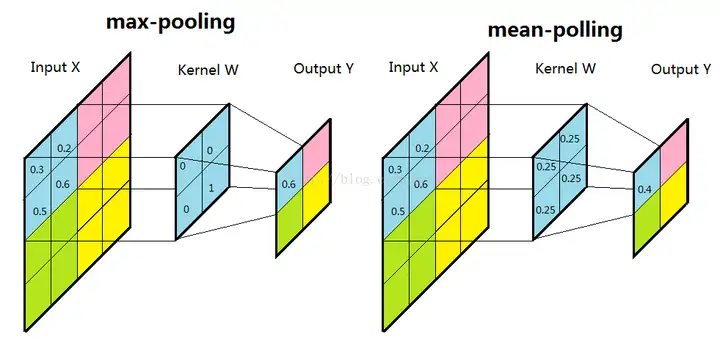
如上图，Max Pooling的优点在于不增加需要调整的参数且通常比其他方法准确，突出特征。而mean Pooling更趋向于平滑。

若没有搞懂就再举个图例，下面是Max pooling，对于每个2*2的窗口选出最大的数作为输出矩阵的相应元素的值，比如输入矩阵第一个2*2窗口中最大的数是6，那么输出矩阵的第一个元素就是6，如此类推。

当然，现在有些人认为池化层并不是必要的，此外，有人发现去除池化层对于生成式模型（generative models）很重要，例如variational autoencoders(VAEs)，generative adversarial networks(GANs)。可能在以后的模型结构中，池化层会逐渐减少或者消失。

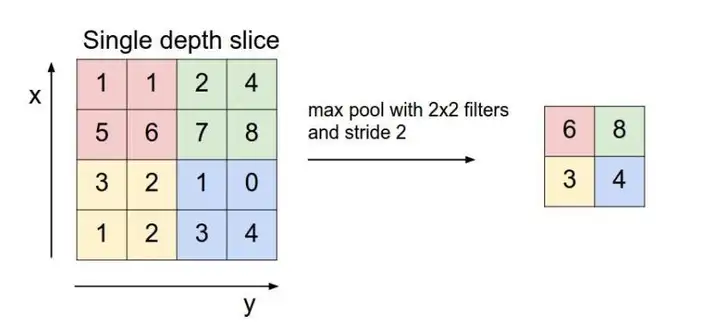
归一化层

在卷积神经网络的结构中，提出了很多不同类型的归一化层，有时候是为了实现在生物大脑中观测到的抑制机制。比如在AlexNet 中的Local Response Nomalization ，但是这些层渐渐都不再流行，因为实践证明它们的效果即使存在，也是极其有限的。

当然，cnn中有很多都用到了batch normalization和dropout，关于这个trick的讲解，可以看下专栏之前的文章。

整体架构

这里列举几种普通常见类型的卷积神经网络结构：

INPUT –> FC/OUT 这其实就是个线性分类器INPUT –> CONV –> RELU –> FC/OUTINPUT –> [CONV –> RELU –> POOL]*2 –> FC –> RELU –> FC/OUTINPUT –> [CONV –> RELU –> CONV –> RELU –> POOL]*3 –> [FC–> RELU]*2 –> FC/OUT

小结

本文主要了解了CNN的各种基础知识，当然，CNN本身各种博大精深，需要仔细研究。下一篇文章，我应该会讲述在imagenet上有关CNN的变体和文章，敬请期待